题目内容
函数y=|x|+3的单调递减区间是 ．
考点：带绝对值的函数
专题：函数的性质及应用
分析：由题意得求出函数的表达式，由分段函数判断函数的单调性，进而顶点答案．
解答：
解：由题意得：
函数f（x）=|x|+3=
，
可得：当x＜0时f′（x）=-1＜0，所以f（x）在（-∞，0）上是减函数．
当x＞0时，f′（x）=1＞0，所以f（x）在（0，+∞）上是增函数．
而x=0在函数的定义域内，
所以函数f（x）=|x|+3的单调递减区间是（-∞，0]．
故答案为：（-∞，0]．
函数f（x）=|x|+3=
|
可得：当x＜0时f′（x）=-1＜0，所以f（x）在（-∞，0）上是减函数．
当x＞0时，f′（x）=1＞0，所以f（x）在（0，+∞）上是增函数．
而x=0在函数的定义域内，
所以函数f（x）=|x|+3的单调递减区间是（-∞，0]．
故答案为：（-∞，0]．
点评：解决此类问题的关键是熟练掌握判断函数单调性的方法，即定义证明与导数证明两种方法，一般是利用导数判断函数的单调性．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
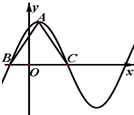
已知函数f（x）的导函数图象如图所示，若△ABC为锐角三角形，则一定成立的是（ ）| A、f（cosA）＜f（cosB） |
| B、f（sinA）＜f（cosB） |
| C、f（sinA）＞f（sinB） |
| D、f（sinA）＞f（cosB） |
函数f（x）=2设M={1，2}，N={a2}，则“N⊆M”是“a=1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |