题目内容
 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E、F分别为A1C1、BC的中点.(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E-ABC的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)证明AB⊥B1BCC1,可得平面ABE⊥B1BCC1;
(2)证明C1F∥平面ABE,只需证明四边形FGEC1为平行四边形,可得C1F∥EG;
(3)利用VE-ABC=
S△ABC•AA1,可求三棱锥E-ABC的体积.
(2)证明C1F∥平面ABE,只需证明四边形FGEC1为平行四边形,可得C1F∥EG;
(3)利用VE-ABC=
| 1 |
| 3 |
解答:
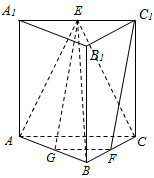 解:(1)证明:∵三棱柱ABC-A1B1C1中,侧棱垂直于底面,
解:(1)证明:∵三棱柱ABC-A1B1C1中,侧棱垂直于底面,
∴BB1⊥AB,
∵AB⊥BC,BB1∩BC=B,BB1,BC?平面B1BCC1,
∴AB⊥平面B1BCC1,
∵AB?平面ABE,
∴平面ABE⊥平面B1BCC1;
(Ⅱ)证明:取AB中点G,连接EG,FG,则
∵F是BC的中点,
∴FG∥AC,FG=
AC,
∵E是A1C1的中点,
∴FG∥EC1,FG=EC1,
∴四边形FGEC1为平行四边形,
∴C1F∥EG,
∵C1F?平面ABE,EG?平面ABE,
∴C1F∥平面ABE;
(3)解:∵AA1=AC=2,BC=1,AB⊥BC,
∴AB=
,
∴VE-ABC=
S△ABC•AA1=
×(
×
×1)×2=
.
 解:(1)证明:∵三棱柱ABC-A1B1C1中,侧棱垂直于底面,
解:(1)证明:∵三棱柱ABC-A1B1C1中,侧棱垂直于底面,∴BB1⊥AB,
∵AB⊥BC,BB1∩BC=B,BB1,BC?平面B1BCC1,
∴AB⊥平面B1BCC1,
∵AB?平面ABE,
∴平面ABE⊥平面B1BCC1;
(Ⅱ)证明:取AB中点G,连接EG,FG,则
∵F是BC的中点,
∴FG∥AC,FG=
| 1 |
| 2 |
∵E是A1C1的中点,
∴FG∥EC1,FG=EC1,
∴四边形FGEC1为平行四边形,
∴C1F∥EG,
∵C1F?平面ABE,EG?平面ABE,
∴C1F∥平面ABE;
(3)解:∵AA1=AC=2,BC=1,AB⊥BC,
∴AB=
| 3 |
∴VE-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
点评:本题考查线面平行、垂直的证明,考查三棱锥E-ABC的体积的计算,正确运用线面平行、垂直的判定定理是关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
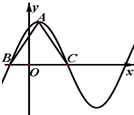
 已知函数f(x)的导函数图象如图所示,若△ABC为锐角三角形,则一定成立的是( )
已知函数f(x)的导函数图象如图所示,若△ABC为锐角三角形,则一定成立的是( )| A、f(cosA)<f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(sinA)>f(cosB) |
 函数f(x)=2
函数f(x)=2