题目内容
8.设x,y为正实数,且x+2y=1,则$\frac{1}{x}+\frac{1}{y}$的最小值为( )| A. | $2+2\sqrt{2}$ | B. | $3+2\sqrt{2}$ | C. | 2 | D. | 3 |
分析 利用“乘1法”和基本不等式即可得出.
解答 解:x,y为正实数,且x+2y=1,
则$\frac{1}{x}+\frac{1}{y}$=($\frac{1}{x}+\frac{1}{y}$)(x+2y)=1+2+$\frac{2y}{x}$+$\frac{x}{y}$≥3+2$\sqrt{\frac{2y}{x}•\frac{x}{y}}$=3+2$\sqrt{2}$,
当且仅当x=$\sqrt{2}$-1,y=$\frac{2-\sqrt{2}}{2}$时取等号,
故则$\frac{1}{x}+\frac{1}{y}$的最小值为3+2$\sqrt{2}$,
故选:B
点评 本题考查了均值不等式求最值,做题时应细心观察,找到变形式子,属于基础题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
18.如图,PA垂直于矩形ABCD所在的平面,则图中与平面PCD垂直的平面是( )
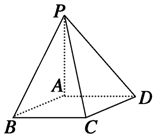

| A. | 平面ABCD | B. | 平面PBC | C. | 平面PAD | D. | 平面PBC |
16.直线x+$\sqrt{3}$y+k=0的倾斜角是( )
| A. | $\frac{5}{6}$π | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
13.向量$\overrightarrow b=(\frac{1}{2},\frac{{\sqrt{3}}}{2})$,$\overrightarrow a•\overrightarrow b=\frac{1}{2}$,则向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
20.在△ABC中,a,b,c分别为内角A,B,C的对边,三边a,b,c成等差数列,且$B=\frac{π}{6}$,则(cosA-cosC)2的值为( )
| A. | $1+\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 0 |
