题目内容

18．如图，PA垂直于矩形ABCD所在的平面，则图中与平面PCD垂直的平面是（　　）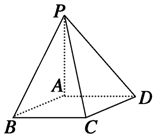
A．平面ABCDB．平面PBCC．平面PADD．平面PBC

分析 由PA⊥平面ABCD，得PA⊥CD，由四边形ABCD为矩形得CD⊥AD，由此得到平面PCD⊥平面PAD．

解答 解：由PA⊥平面ABCD，得PA⊥CD，
由四边形ABCD为矩形得CD⊥AD，
从而有CD⊥平面PAD，CD?平面PCD，
所以平面PCD⊥平面PAD．
故选：C．

点评 本题考查与已知平面垂直的平面的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
8．无锡市政府决定规划地铁三号线：该线起於惠山区惠山城铁站，止於无锡新区硕放空港产业园内的无锡机场站，全长28公里，目前惠山城铁站和无锡机场站两个站点已经建好，余下的工程是在已经建好的站点之间铺设轨道和等距离修建停靠站．经有关部门预算，修建一个停靠站的费用为6400万元，铺设距离为x公里的相邻两个停靠站之间的轨道费用为400x3+20x万元．设余下工程的总费用为f（x）万元．（停靠站位于轨道两侧，不影响轨道总长度）
（1）试将f（x）表示成x的函数；
（2）需要建多少个停靠站才能使工程费用最小，并求最小值．
9．（1）已知角α的终边上一点P的坐标为$（-\sqrt{3}，2）$，求sinα，cosα和tanα．
（2）在[0°，720°]中与-21°16′终边相同的角有哪些？
6．根据条件回答下列问题：
（1）求函数y=lg（tanx）的定义域；
（2）求函数$y=\frac{3sinx+1}{sinx-2}$的值域．
13．函数$f（x）=\frac{3^x}{{{3^x}+\sqrt{3}}}$，则$f（\frac{1}{2016}）+f（\frac{2}{2016}）+…+f（\frac{2015}{2016}）+f（\frac{2016}{2016}）$=1009-$\frac{\sqrt{3}}{2}$．
3．已知函数f（x）的定义域为R，对任意实数x，y满足f （x+y）=f（x）+f （y）+0.5，且f （0.5）=0，当x＞0.5时，f（x）＞0，给出以下结论：
①f （0）=-0.5；
②f （-1）=-1.5；   
③f（x）为R上的减函数；   
④f（x）+0.5为奇函数；
⑤f（x）+1为偶函数．
其中正确结论的序号是①②④．
10．已知向量$\overrightarrow a=（cosα，sinα）$，$\overrightarrow b=（cosβ，sinβ）$，且$α-β=\frac{2π}{3}$，则$\overrightarrow a$与$\overrightarrow a+\overrightarrow b$的夹角为（　　）
A．$\frac{π}{3}$B．$\frac{π}{2}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$
7．已知函数f（x）=x2+bx-alnx（a≠0）
（1）当b=0时，讨论函数f（x）的单调性；
（2）若x=2是函数f（x）的极值点，1是函数f（x）的一个零点，求a+b的值；
（3）若对任意b∈[-2，-1]，都存在x∈（1，e），使得f（x）＜0成立，求实数a的取值范围．
8．设x，y为正实数，且x+2y=1，则$\frac{1}{x}+\frac{1}{y}$的最小值为（　　）
A．$2+2\sqrt{2}$B．$3+2\sqrt{2}$C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网