题目内容
20.在△ABC中,a,b,c分别为内角A,B,C的对边,三边a,b,c成等差数列,且$B=\frac{π}{6}$,则(cosA-cosC)2的值为( )| A. | $1+\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 0 |
分析 三边a,b,c成等差数列,可得2b=a+c,利用正弦定理可得:2sinB=sinA+sinC,即sinA+sinC=1,设cosA-cosC=m,平方相加即可得出.
解答 解:∵三边a,b,c成等差数列,
∴2b=a+c,
利用正弦定理可得:2sinB=sinA+sinC,
∴sinA+sinC=2sin$\frac{π}{6}$=1,
设cosA-cosC=m,
则平方相加可得:2-2cos(A+C)=1+m2,
∴m2=2cosB+1=$\sqrt{3}+1$.
故选:A.
点评 本题考查了等差数列的通项公式性质、正弦定理、同角三角函数基本关系式、和差公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.已知向量$\overrightarrow a=(cosα,sinα)$,$\overrightarrow b=(cosβ,sinβ)$,且$α-β=\frac{2π}{3}$,则$\overrightarrow a$与$\overrightarrow a+\overrightarrow b$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
8.设x,y为正实数,且x+2y=1,则$\frac{1}{x}+\frac{1}{y}$的最小值为( )
| A. | $2+2\sqrt{2}$ | B. | $3+2\sqrt{2}$ | C. | 2 | D. | 3 |
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线平行于直线l:3x-2y+3$\sqrt{13}$=0,且双曲线的一个焦点在直线l上,则双曲线方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{5{x}^{2}}{16}$-$\frac{5{y}^{2}}{9}$=1 |
12.函数f(x)=2-$\frac{3}{x}$在区间[1,3]上的最大值是( )
| A. | 2 | B. | 3 | C. | -1 | D. | 1 |
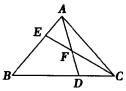 如图,在△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于点F,则$\frac{EF}{FC}+\frac{AF}{FD}$的值为$\frac{3}{2}$.
如图,在△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于点F,则$\frac{EF}{FC}+\frac{AF}{FD}$的值为$\frac{3}{2}$.