题目内容
13.向量$\overrightarrow b=(\frac{1}{2},\frac{{\sqrt{3}}}{2})$,$\overrightarrow a•\overrightarrow b=\frac{1}{2}$,则向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
分析 根据投影公式$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$,代值计算即可
解答 解:由定义,向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{1}{2}$,
故选:A.
点评 本题主要考查向量投影的定义及求解的方法,公式与定义两者要灵活运用.解答关键在于要求熟练应用公式.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
1.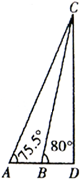 2016年春节期间,小明和小张去上海旅游,参观了东方明珠塔,两人为了测量它的高度,站在A处测得塔尖C的仰角为75.5°,前进38.5m后到达B处,没得塔尖C的仰角为80°,如图所示(其中D为塔底),则东方明珠塔的高度约为( )(参考数据:sin80°≈0.985,sin75.5°≈0.968,sin4.5°≈0.078)
2016年春节期间,小明和小张去上海旅游,参观了东方明珠塔,两人为了测量它的高度,站在A处测得塔尖C的仰角为75.5°,前进38.5m后到达B处,没得塔尖C的仰角为80°,如图所示(其中D为塔底),则东方明珠塔的高度约为( )(参考数据:sin80°≈0.985,sin75.5°≈0.968,sin4.5°≈0.078)
 2016年春节期间,小明和小张去上海旅游,参观了东方明珠塔,两人为了测量它的高度,站在A处测得塔尖C的仰角为75.5°,前进38.5m后到达B处,没得塔尖C的仰角为80°,如图所示(其中D为塔底),则东方明珠塔的高度约为( )(参考数据:sin80°≈0.985,sin75.5°≈0.968,sin4.5°≈0.078)
2016年春节期间,小明和小张去上海旅游,参观了东方明珠塔,两人为了测量它的高度,站在A处测得塔尖C的仰角为75.5°,前进38.5m后到达B处,没得塔尖C的仰角为80°,如图所示(其中D为塔底),则东方明珠塔的高度约为( )(参考数据:sin80°≈0.985,sin75.5°≈0.968,sin4.5°≈0.078)| A. | 456m | B. | 438m | C. | 350m | D. | 471m |
8.设x,y为正实数,且x+2y=1,则$\frac{1}{x}+\frac{1}{y}$的最小值为( )
| A. | $2+2\sqrt{2}$ | B. | $3+2\sqrt{2}$ | C. | 2 | D. | 3 |
2.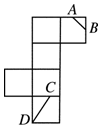 如图所示,是一个正方体的表面展开图,A、B、C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为( )
如图所示,是一个正方体的表面展开图,A、B、C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为( )
 如图所示,是一个正方体的表面展开图,A、B、C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为( )
如图所示,是一个正方体的表面展开图,A、B、C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为( )| A. | $\frac{{\sqrt{2}}}{5}$ | B. | $\frac{{\sqrt{3}}}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |