题目内容
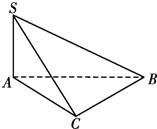 已知△ABC中,∠BAC=90°,SA⊥面ABC,且SA=3,AB=AC=4.
已知△ABC中,∠BAC=90°,SA⊥面ABC,且SA=3,AB=AC=4.(1)求SC与平面SAB所成角的余弦值;
(2)试判断△SBC的形状,说明理由.
考点:直线与平面所成的角,三角形的形状判断
专题:计算题,空间位置关系与距离,空间角
分析:(1)首先根据线面垂直的性质和判定定理,得到AC⊥面SAB,则∠CSA则为SC与平面SAB所成角.求∠CSA的大小可以通过解直角三角形知识求解;
(2)要判定△SBC的形状,可通过解直角三角形,计算SB,SC,BC,再由解三角形的知识,即可判断.
(2)要判定△SBC的形状,可通过解直角三角形,计算SB,SC,BC,再由解三角形的知识,即可判断.
解答:
解:(1)由∠BAC=90°,则AB⊥AC,
SA⊥面ABC,则SA⊥AC,
又AB∩SA=A,则有AC⊥面SAB,
则∠CSA则为SC与平面SAB所成角.
在直角△ACS中,AS=3,AC=4,SC=5,
则cos∠CSA=
,
故SC与平面SAB所成角的余弦值
;
(2)△SBC为等腰三角形或锐角三角形.
由于SA⊥面ABC,
则SA⊥AB,则有SB=SC=5,
在直角△ABC中,BC=4
,
cos∠CSB=
>0,
则∠CSB为锐角三角形,
故三角形SBC为等腰三角形或锐角三角形.
SA⊥面ABC,则SA⊥AC,
又AB∩SA=A,则有AC⊥面SAB,
则∠CSA则为SC与平面SAB所成角.
在直角△ACS中,AS=3,AC=4,SC=5,
则cos∠CSA=
| 3 |
| 5 |
故SC与平面SAB所成角的余弦值
| 3 |
| 5 |
(2)△SBC为等腰三角形或锐角三角形.
由于SA⊥面ABC,
则SA⊥AB,则有SB=SC=5,
在直角△ABC中,BC=4
| 2 |
cos∠CSB=
52+52-(4
| ||
| 2×5×5 |
则∠CSB为锐角三角形,
故三角形SBC为等腰三角形或锐角三角形.
点评:本题考查的知识点:线面垂直的判定和性质定理,线面夹角的转化,解直角三角形,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=ex-1,g(x)=-x2+4x-4.若有f(a)=g(b),则b的取值范围为( )
A、[2-
| ||||
B、(2-
| ||||
| C、[1,3] | ||||
| D、(1,3) |
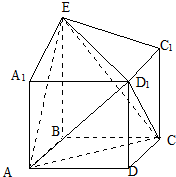 在如图所示的几何体中,底面ABCD为菱形,∠BAD=60°,AA1
在如图所示的几何体中,底面ABCD为菱形,∠BAD=60°,AA1