题目内容
是否存在正整数a,使得1n+3n+(2n-1)n<
(an)n对一切正整数n均成立?若存在,求a的最小值,若不存在,请说明理由.
| ||
| e-1 |
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:设t(x)=ex-x-1,则t′(x)=ex-1,从而得到ex≥x+1,取x=-
,用累加法得到得(
)n+(
)n+…+(
)n<e-
+e-
+…+e-
<
.
由此能够推导出存在正整数a=2,使得1n+3n+…+(2n-1)n<•(an)n.
| i |
| 2n |
| 1 |
| 2n |
| 3 |
| 2n |
| 2n-1 |
| 2n |
| 2n-1 |
| 2 |
| 2n-3 |
| 2 |
| 1 |
| 2 |
| ||
| e-1 |
由此能够推导出存在正整数a=2,使得1n+3n+…+(2n-1)n<•(an)n.
解答:
解:设t(x)=ex-x-1,
则t′(x)=ex-1,令t′(x)=0得:x=0.
在x<0时t′(x)<0,f(x)递减;在x>0时t′(x)>0,f(x)递增.
∴t(x)最小值为t(0)=0,故ex≥x+1,
取x=-
,
得1-
≤e-
,即(
)n≤e-
,
累加得(
)n+(
)n+…+(
)n<e-
+e-
+…+e-
=
<
.
∴1n+3n+…+(2n-1)n<
•(2n)n,
故存在正整数a=2.使得1n+3n+…+(2n-1)n<
•(an)n.
则t′(x)=ex-1,令t′(x)=0得:x=0.
在x<0时t′(x)<0,f(x)递减;在x>0时t′(x)>0,f(x)递增.
∴t(x)最小值为t(0)=0,故ex≥x+1,
取x=-
| i |
| 2n |
得1-
| i |
| 2n |
| i |
| 2n |
| 2n-i |
| 2n |
| i |
| 2 |
累加得(
| 1 |
| 2n |
| 3 |
| 2n |
| 2n-1 |
| 2n |
| 2n-1 |
| 2 |
| 2n-3 |
| 2 |
| 1 |
| 2 |
e-
| ||
| 1-e-1 |
| ||
| e-1 |
∴1n+3n+…+(2n-1)n<
| ||
| e-1 |
故存在正整数a=2.使得1n+3n+…+(2n-1)n<
| ||
| e-1 |
点评:本题考查不等式恒成立问题,探索满足条件的实数的最小值的求法,综合性强,难度大,解答的关键是合理地运算导数性质进行等价转化,是压轴题.

练习册系列答案
相关题目
已知点P是△ABC的内心(三个内角平分线交点)、外心(三条边的中垂线交点)、重心(三条中线交点)、垂心(三个高的交点)之一,且满足2
•
=
2-
2
,则点P一定是△ABC的( )
| AP |
| BC |
| AC |
| AB |
,则点P一定是△ABC的( )
| A、内心 | B、外心 | C、重心 | D、垂心 |
函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A)有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t度低调函数.已知定义域为[0,+∞)的函数f(x)=-|mx-3|,且f(x)为[0,+∞)上的6度低调函数,那么实数m的取值范围是( )
| A、[0,1] |
| B、[1,+∞) |
| C、(-∞,0) |
| D、(-∞,0]∪[1,+∞) |
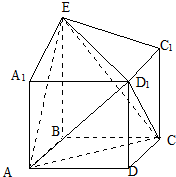 在如图所示的几何体中,底面ABCD为菱形,∠BAD=60°,AA1
在如图所示的几何体中,底面ABCD为菱形,∠BAD=60°,AA1