题目内容
函数f(x)=x-
的定义域为(0,1].
(1)若函数y=f(x)在定义域上是减函数,求a的取值范围;
(2)求函数y=f(x)在x∈(0,1]上的最值.并求出函数取最值时x的值.
| a |
| x |
(1)若函数y=f(x)在定义域上是减函数,求a的取值范围;
(2)求函数y=f(x)在x∈(0,1]上的最值.并求出函数取最值时x的值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:函数的性质及应用,导数的综合应用
分析:(1)先求出函数的导数,通过讨论a的范围,得到函数单调区间,从而求出a的范围;
(2)通过讨论a的范围,得到函数的单调性,从而求出函数f(x)的最值.
(2)通过讨论a的范围,得到函数的单调性,从而求出函数f(x)的最值.
解答:
解:(1)∵f′(x)=1+
,
a≥0时,f′(x)>0,f(x)在(0,1]递增,不合题意,
a<0时,令f′(x)<0,解得:-
<x<
,而0<x≤1,
∴
≥1,即a≤-1时,f(x)在(0,1]上递减;
(2)a≥0时,f(x)在(0,1]递增,
f(x)无最小值,f(x)的最大值是f(1)=1-a,
-1<a<0时,f(x)在(0,
)递减,在(
,1]递增,
∴f(x)的最小值是f(
)=0,f(x)无最大值.
| a |
| x2 |
a≥0时,f′(x)>0,f(x)在(0,1]递增,不合题意,
a<0时,令f′(x)<0,解得:-
| -a |
| -a |
∴
| -a |
(2)a≥0时,f(x)在(0,1]递增,
f(x)无最小值,f(x)的最大值是f(1)=1-a,
-1<a<0时,f(x)在(0,
| -a |
| -a |
∴f(x)的最小值是f(
| -a |
点评:本题考查了函数的单调性问题,考查了函数的最值问题,考查了分类讨论,是一道中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知函数f(x)=ex-1,g(x)=-x2+4x-4.若有f(a)=g(b),则b的取值范围为( )
A、[2-
| ||||
B、(2-
| ||||
| C、[1,3] | ||||
| D、(1,3) |
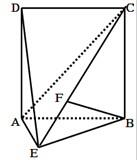 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE,求DE与平面AEC所成夹角的正弦值.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE,求DE与平面AEC所成夹角的正弦值.