Question

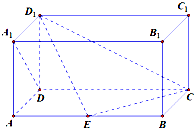如图，在长方体ABCD-A₁B₁C₁D₁中，AD=AA₁=1，AB=2，点E在棱AB上．
（1）求异面直线D₁E与A₁D所成的角；
（2）若二面角D₁-EC-D的大小为45°，求直线BC₁与面D₁EC所成的角的正切．．

Answer 1

考点：与二面角有关的立体几何综合题,异面直线及其所成的角

专题：空间位置关系与距离,空间角

分析：（1）以D为原点，建立空间直角坐标系，利用向量法能求出异面直线D₁E与A₁D所成的角．
（2）求出平面D₁EC的法向量

n

=（

3

，1，2），由此利用向量法能求出直线BC₁与面D₁EC所成的角的正切．

解答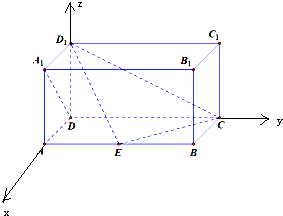： 解：（1）如图，以D为原点，建立空间直角坐标系，
则D₁（0，0，1），设E（1，t，0），0≤t≤2，
A₁（1，0，1），D（0，0，0），C（0，2，0）

D1E

=（1，t，-1），

A1D

=（-1，0，-1），
cos＜

D1E

，

A1D

＞=

-1+0+1

3 • 2

=0，
∴异面直线D₁E与A₁D所成的角为90°．
（2）

D1E

=（1，t，-1），

D1C

=（0，2，-1），
设平面D₁EC的法向量

n

=（x，y，z），
则

n • D1E =x+ty-z=0 n • D1C =2y-z=0

，
取y=1，得

n

=(2-t，1，2)，
又平面ECD的法向量

m

=（0，0，1），二面角D₁-EC-D的大小为45°，
∴cos45°=cos＜

m

，

n

＞=

2

(2-t)2+5

，
解得t=2-

3

，或t=2+

3

（舍），
∴

n

=（

3

，1，2），
B（1，2，0），C₁（0，2，1），

BC1

=（-1，0，1），
设直线BC₁与面D₁EC所成的角为θ，
sinθ=|cos＜

BC1

，

n

＞|=|

- 3 +2

8 • 2

|=

2- 3

4

，
∴tanθ=

(2- 3 ) 9+4 3

9+4 3

．
∴直线BC₁与面D₁EC所成的角的正切为

(2- 3 ) 9+4 3

9+4 3

．

点评：本题考查异面直线所成的角的求法，考查直线与平面所成角的正切值的求法，解题时要认真审题，注意向量法的合理运用．