题目内容
求函数y=x2-ax+1在区间[0,1]上的最小值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:由条件利用二次函数的性质,分对称轴在区间[0,1]的左侧、中间、由侧三种情况,分别求得函数的最小值.
解答:
解:函数y=f(x)=x2-ax+1=(x-
)2+1-
,在区间[0,1]上,
当
<0时,函数的最小值为f(0)=1;当0≤
≤1时,函数的最小值为f(
)=1-
;
当
>1时,函数的最小值为f(1)=2-a.
| a |
| 2 |
| a2 |
| 4 |
当
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
当
| a |
| 2 |
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属基础题.

练习册系列答案
相关题目
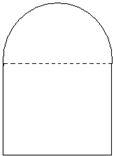 某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?
某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?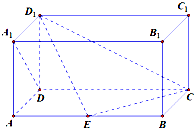 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.