题目内容
若直线l1,l2的倾斜角为直线y=
x+1的倾斜角的一半,且满足下列条件的直线l1,l2的方程;
(1)直线l1经过点(-4,1);
(2)直线l2在y轴上的截距为-10.
| 3 |
(1)直线l1经过点(-4,1);
(2)直线l2在y轴上的截距为-10.
考点:直线的一般式方程
专题:直线与圆
分析:(1)由已知条件利用正切函数二倍角公式求出直线l1,l2的斜率k=
,由此利用点斜式方程能求出直线方程.
(2)利用斜截式方程能求出直线方程.
| ||
| 3 |
(2)利用斜截式方程能求出直线方程.
解答:
解:(1)∵直线l1,l2的倾斜角为直线y=
x+1的倾斜角的一半,
∴设直线y=
x+1的倾斜角为2α,l2的倾斜角为α,α为锐角,
则tan2α=
=
,
解得tanα=
,或tanα=-
(舍),
∴直线l1,l2的斜率k=
,
∵直线l1经过点(-4,1),
∴直线l1的方程为y-1=
(x+4),
整理得
x-3y+4
+3=0.
(2)∵直线l2在y轴上的截距为-10.,
∴直线l2的方程为y=
x-10,
整理,得x-
y-10
=0.
| 3 |
∴设直线y=
| 3 |
则tan2α=
| 2tanα |
| 1-tan2α |
| 3 |
解得tanα=
| ||
| 3 |
| 3 |
∴直线l1,l2的斜率k=
| ||
| 3 |
∵直线l1经过点(-4,1),
∴直线l1的方程为y-1=
| ||
| 3 |
整理得
| 3 |
| 3 |
(2)∵直线l2在y轴上的截距为-10.,
∴直线l2的方程为y=
| ||
| 3 |
整理,得x-
| 3 |
| 3 |
点评:本题考查直线方程的求法,是基础题,解题时要注意正切函数的二倍角公式的合理运用.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
函数f(x)=2lnx+2x-5的零点个数为( )
| A、1 | B、2 | C、0 | D、3 |
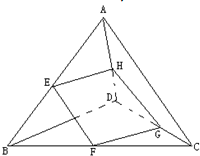 已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.
已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.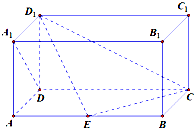 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.