题目内容
设函数f(x,y)=(1+
)x(m>0,y>0),若f(4,y)=a0+
+
+
+
且a3=32,求∑ai.
| m |
| y |
| a1 |
| y |
| a2 |
| y2 |
| a3 |
| y3 |
| a4 |
| y4 |
考点:指数函数的图像与性质
专题:函数的性质及应用,二项式定理
分析:令x=4,y=1,则f(4,1)=(1+m)4,再根据a3=32,求得m的值,再根二项式定理,求的答案.
解答:
解:令x=4,y=1,
则f(4,1)=(1+m)4,
∴a3=
m3,
∵f(4,y)=a0+
+
+
+
且a3=32,
当y=1时,
∴f(4,1)=a0 +a1 +a2 +a3 +a4,
∴a3=
m3=32,
解得m=2,
∴∑ai=a1 +a2 +…+an=f(n,1)-a0=(1+2)n-1=3n-1
则f(4,1)=(1+m)4,
∴a3=
| C | 3 4 |
∵f(4,y)=a0+
| a1 |
| y |
| a2 |
| y2 |
| a3 |
| y3 |
| a4 |
| y4 |
当y=1时,
∴f(4,1)=a0 +a1 +a2 +a3 +a4,
∴a3=
| C | 3 4 |
解得m=2,
∴∑ai=a1 +a2 +…+an=f(n,1)-a0=(1+2)n-1=3n-1
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于中档题.

练习册系列答案
相关题目
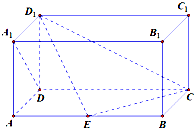 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.