题目内容
解关于x的方程:x4-2ax2-x+a2-a=0(-0.25≤a<0.75).
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:将原方程化为以a为未知数的形式,因式分解,进而解方程.
解答:
解:原方程可化为:a2-(2x2+1)a+x4-x=0,
即:[a-x(x-1)][a-(x2+x+1)]=0,
①当a-x(x-1)=0时,x=
±
;
②当a-(x2+x+1)=0时
△=1-4(1-a)=4a-3,
∵-0.25≤a<0.75,
∴△<0,
则方程无解.
综上所述,x=
±
(-0.25≤a<0.75).
即:[a-x(x-1)][a-(x2+x+1)]=0,
①当a-x(x-1)=0时,x=
| 1 |
| 2 |
| ||
| 2 |
②当a-(x2+x+1)=0时
△=1-4(1-a)=4a-3,
∵-0.25≤a<0.75,
∴△<0,
则方程无解.
综上所述,x=
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查了换参数思考,将原方程看成以a为未知数的方程是本题解决的关键.

练习册系列答案
相关题目
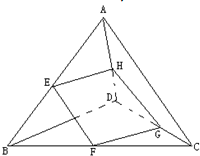 已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.
已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.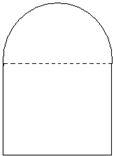 某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?
某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?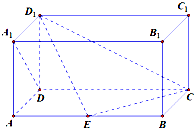 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.