题目内容
函数f（x）=x3-15x2-33x+6的单调递增区间为 ．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：由已知得f′（x）=3x2-30x-33，再由f′（x）＞0，能求出函数f（x）=x3-15x2-33x+6的单调递增区间．
解答：
解：∵f（x）=x3-15x2-33x+6，
∴f′（x）=3x2-30x-33，
由f′（x）＞0，得x＞11或x＜-1．
∴函数f（x）=x3-15x2-33x+6的单调递增区间为（-∞，-1），（11，+∞）．
故答案为：（-∞，-1），（11，+∞）．
∴f′（x）=3x2-30x-33，
由f′（x）＞0，得x＞11或x＜-1．
∴函数f（x）=x3-15x2-33x+6的单调递增区间为（-∞，-1），（11，+∞）．
故答案为：（-∞，-1），（11，+∞）．
点评：本题考查函数的增区间的求法，是基础题，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
M，N在圆C：x2+y2+2x-4y=0上，且点M，N关于直线3x+y+a=0对称，则a=（ ）
| A、-1 | B、-3 | C、3 | D、1 |
已知二次函数y=-x2+1，则它与x轴所围图形的面积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
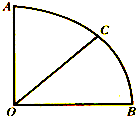如图，在圆心角为90°的扇形中以圆心．为起点作射线OC，则使得∠AOC与∠BOC都不大于60°的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
若f（x）=cosx在[-b，-a]上是增函数，则f（x）在[a，b]上是（ ）
| A、奇函数 | B、偶函数 |
| C、减函数 | D、增函数 |