Question

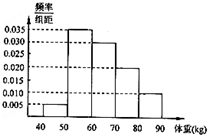从某地区随机抽取100名高中男生，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．若要从体重在[60，70），[70，80），[80，90]三组内的男生中，用分层抽样的方法选取12人参加一项活动，再从这12人中选两人当正、副队长，则这两人体重不在同一组内的概率为（　　）

• A、

  1

  3

• B、

  1

  4

• C、

  2

  5

• D、

  2

  3

Answer 1

考点：频率分布直方图

专题：图表型

分析：先求出这三组内的男生中抽取的人数，根据所有的选法有这两人身高不在同一组内的选法有44种，由此求得两人身高不在同一组内的概率．

解答： 在[60，70），[70，80），[80，90]三组内的男生中抽取的人数之比为 0.3：0.2：0.1=3：2：1，
故这三组内的男生中抽取的人数分别为12×

3

3+2+1

=6，12×

2

3+2+1

=4，12×

1

3+2+1

=2
所有的选法有

C

2 12

=66种，
这两人身高不在同一组内的选法有 6×4+6×2+4×2=44种，
故这两人身高不在同一组内的概率为

44

66

=

2

3

故选D

点评：本题主要考查等可能事件的概率，频率分步直方图的应用，属于中档题．