题目内容
若关于x的不等式x2+ax-2＜0的解集为{x|-1＜x＜2}，则实数a=（ ）
| A、-1 | B、1 | C、-2 | D、2 |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：利用一元二次不等式的解集与相应的一元二次方程的实数根的关系、根与系数的关系即可得出．
解答：
解：∵关于x的不等式x2+ax-2＜0的解集为{x|-1＜x＜2}，
∴-1+2=-a，
解得a=-1．
故选：A．
∴-1+2=-a，
解得a=-1．
故选：A．
点评：本题考查了一元二次不等式的解集与相应的一元二次方程的实数根的关系、根与系数的关系，属于基础题．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
在复平面内，复数
-
i3对应的点位于（ ）
| 1 |
| 1+i |
| 1 |
| 4 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
复数Z满足（3-4i）Z=|4+3i|，则Z的虚部为（ ）
| A、4i | ||
| B、4 | ||
C、
| ||
D、
|
函数y=sinx在点x=
处的导数是（ ）
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
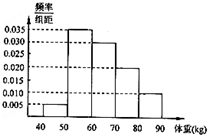从某地区随机抽取100名高中男生，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．若要从体重在[60，70），[70，80），[80，90]三组内的男生中，用分层抽样的方法选取12人参加一项活动，再从这12人中选两人当正、副队长，则这两人体重不在同一组内的概率为（ ）