题目内容
一个质量为1kg的物体作直线运动，设运动距离s（单位：m）与时间t（单位：s）的关系可用函数s（t）=（2t-1）2表示，并且物体的动能Ek=
mv2，则物体开始运动后第2s时的动能是（ ）
| 1 |
| 2 |
| A、18J | B、36J |
| C、72J | D、144J |
考点：定积分
专题：计算题
分析：对路程关于时间的函数求导，得到v（2），然后代入动能公式得答案．
解答：
解：由s（t）=（2t-1）2，得：
v（t）=s′（t）=2×（2t-1）×2=8t-4，
∴v（2）=12．
∴物体开始运动后第2s时的动能是
×1×122=72（J）．
故选：C．
v（t）=s′（t）=2×（2t-1）×2=8t-4，
∴v（2）=12．
∴物体开始运动后第2s时的动能是
| 1 |
| 2 |
故选：C．
点评：本题考查了导数的应用，解答的关键在于明确速度是路程关于时间的一阶导数，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
函数y=sinx在点x=
处的导数是（ ）
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
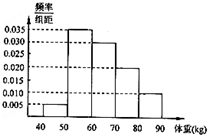从某地区随机抽取100名高中男生，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．若要从体重在[60，70），[70，80），[80，90]三组内的男生中，用分层抽样的方法选取12人参加一项活动，再从这12人中选两人当正、副队长，则这两人体重不在同一组内的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
将函数y=sin（x+
）图象上各点的横坐标缩短到原来的
倍（纵坐标不变），再向右平移
个单位，那么所得图象的一条对称轴方程为（ ）
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|
命题P：“若x2=1，则x=1”，在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |