题目内容
已知正方形ABCD的边长为2,E、F、G、H分别是边AB、BC、CD、DA的中点.
(1)从C、D、E、F、G、H这六个点中,随机选取两个点,记这两个点之间的距离的平方为ξ,求概率P(ξ≤4).
(2)在正方形ABCD内部随机取一点P,求满足|PE|<2的概率.
(1)从C、D、E、F、G、H这六个点中,随机选取两个点,记这两个点之间的距离的平方为ξ,求概率P(ξ≤4).
(2)在正方形ABCD内部随机取一点P,求满足|PE|<2的概率.
考点:几何概型,互斥事件的概率加法公式
专题:计算题,概率与统计
分析:(1)从C、D、E、F、G、H这六个点中,随机选取两个点,共有
=15种,其中DE,DF,CE,CH两个点之间的距离的平方为5,不满足题意,即可得出结论.
(2)根据几何概型的概率计算公式,分别求出正方形的面积和满足|PE|<2的正方形内部的点P的集合的面积即可得出;
| C | 2 6 |
(2)根据几何概型的概率计算公式,分别求出正方形的面积和满足|PE|<2的正方形内部的点P的集合的面积即可得出;
解答:
解:(1)从C、D、E、F、G、H这六个点中,随机选取两个点,共有
=15种,其中DE,DF,CE,CH两个点之间的距离的平方为5,不满足题意,
∴P(ξ≤4)=1-
=
…(6分)
(2)这是一个几何概型.所有点P构成的平面区域是正方形ABCD的内部,其面积是2×2=4.
满足|PE|<2的点P构成的平面区域是以E为圆心,2为半径的圆的内部与正方形ABCD内部的公共部分,它可以看作是由一个以E为圆心、2为半径、圆心角为
的扇形的内部与两个直角边分别为1和
的直角三角形内部构成.
其面积是
×
×22+2×
×1×
=
+
.
所以满足|PE|<2的概率为
=
+
…(12分)
| C | 2 6 |
∴P(ξ≤4)=1-
| 4 |
| 15 |
| 11 |
| 15 |
(2)这是一个几何概型.所有点P构成的平面区域是正方形ABCD的内部,其面积是2×2=4.
满足|PE|<2的点P构成的平面区域是以E为圆心,2为半径的圆的内部与正方形ABCD内部的公共部分,它可以看作是由一个以E为圆心、2为半径、圆心角为
| π |
| 3 |
| 3 |
其面积是
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| 2π |
| 3 |
| 3 |
所以满足|PE|<2的概率为
| ||||
| 4 |
| π |
| 6 |
| ||
| 4 |
点评:本题考查了几何概型,正确求出试验的全部结果所构成的区域的面积和长度以及要求的事件的区域的面积和长度是解题的关键.

练习册系列答案
相关题目
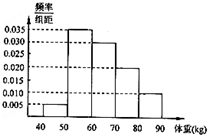 从某地区随机抽取100名高中男生,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从体重在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取12人参加一项活动,再从这12人中选两人当正、副队长,则这两人体重不在同一组内的概率为( )
从某地区随机抽取100名高中男生,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从体重在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取12人参加一项活动,再从这12人中选两人当正、副队长,则这两人体重不在同一组内的概率为( )