题目内容
下列对应为从A到B的一一映射的为( )
| A、A={x|x<0且x∈R},B={y|y>0且y∈R},f:x→-x+1 | ||
B、A=R,B={y|y∈R且y≠0},f:x→
| ||
C、A={x|x>0且x∈R},B={y|y≥0且y∈R},f:x→
| ||
| D、A=R,B=R,f:x→2x+3 |
考点:映射
专题:计算题,函数的性质及应用
分析:判断一个对应关系是否为一一映射,要从基本概念入手,看是否满足一一映射的条件,从而得出结论.
解答:
解:A选项,B中,-x+1>0,则x<1,所以不是一一映射;
B选项,元素0在B中没有像与之对应,所以不是映射;
C选项,0没有原像,所以不是一一映射;
D选项,A中的每一个元素在B中都有唯一元素与之对应,A中的不同元素在B中的像也不同,且B中的元素在A中都有原像,所以是一一映射.
故选:D.
B选项,元素0在B中没有像与之对应,所以不是映射;
C选项,0没有原像,所以不是一一映射;
D选项,A中的每一个元素在B中都有唯一元素与之对应,A中的不同元素在B中的像也不同,且B中的元素在A中都有原像,所以是一一映射.
故选:D.
点评:本题主要考查映射、一一映射的定义,属于基础题.

练习册系列答案
相关题目
复数Z满足(3-4i)Z=|4+3i|,则Z的虚部为( )
| A、4i | ||
| B、4 | ||
C、
| ||
D、
|
函数y=sinx在点x=
处的导数是( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
在(-π,4π)内与-
终边相同的角有( )个.
| 5π |
| 4 |
| A、0 | B、1 | C、2 | D、3 |
已知全集U=R,集合A={x|x2≥3},B={x|1<x<3},则A∪(∁UB)=( )
| A、R | ||||
B、{x|x≤-
| ||||
C、{x|x≤1或x≥
| ||||
D、{x|x≤-
|

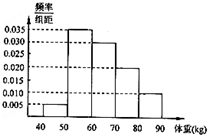 从某地区随机抽取100名高中男生,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从体重在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取12人参加一项活动,再从这12人中选两人当正、副队长,则这两人体重不在同一组内的概率为( )
从某地区随机抽取100名高中男生,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从体重在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取12人参加一项活动,再从这12人中选两人当正、副队长,则这两人体重不在同一组内的概率为( )