题目内容

已知x=log23-log2
3
，y=log0.5π，z=0.9-1.1，则（　　）
A、x＜y＜z
B、z＜y＜x
C、y＜z＜x
D、y＜x＜z
考点：对数的运算性质,对数值大小的比较
专题：函数的性质及应用
分析：利用对数函数和指数函数的单调性即可得出．
解答： 解：∵y=log0.5π＜log0.51=0，
0＜x=log2
3
3
=log2
3
＜1，
z=0.9-1.1＞0.90=1．
∴y＜x＜z．
故选：D．
点评：本题考查了对数函数和指数函数的单调性，属于基础题．
练习册系列答案
相关题目
复数Z满足（3-4i）Z=|4+3i|，则Z的虚部为（　　）
A、4i
B、4
C、
4
5
i
D、
4
5
已知全集U=R，集合A={x|x2≥3}，B={x|1＜x＜3}，则A∪（∁UB）=（　　）
A、R
B、{x|x≤-
3
或x≥
3
}
C、{x|x≤1或x≥
3
}
D、{x|x≤-
3
或x≥3}
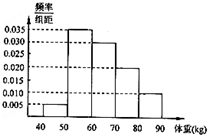从某地区随机抽取100名高中男生，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．若要从体重在[60，70），[70，80），[80，90]三组内的男生中，用分层抽样的方法选取12人参加一项活动，再从这12人中选两人当正、副队长，则这两人体重不在同一组内的概率为（　　）
A、
1
3
B、
1
4
C、
2
5
D、
2
3
有两张卡片，一张的正反面分别写着数字0与1，另一张的正反面分别写着数字2与3，将两张卡片排在一起组成两位数，则所组成的两位数为奇数的概率是（　　）
A、
1
6
B、
1
3
C、
1
2
D、
3
8
将函数y=sin（x+
π
6
）图象上各点的横坐标缩短到原来的
1
2
倍（纵坐标不变），再向右平移
π
3
个单位，那么所得图象的一条对称轴方程为（　　）
A、x=-
π
4
B、x=-
π
2
C、x=
π
8
D、x=
π
4
命题P：“若x2=1，则x=1”，在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（　　）
A、0B、1C、2D、3
已知函数f（x）=sinωx+cos（ωx+
π
6
），其中x∈R，ω为正常数．
（1）当ω=2时，求f（
π
3
）的值；
（2）记f（x）的最小正周期为T，若f（
π
3
）=1，求T的最大值．
已知实数t，若存在t∈[
1
2
，3]使得不等式|t-1|-|2t-5|≥|x-1|+|x-2|成立，求实数x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网