题目内容
正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为
,则直线BC1与平面AA1B1B所成角的正切值为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与平面所成的角
专题:空间角
分析:取A1B1的中点D,连接C1D,BD,BC1,则可得∠C1BD即为直线BC1与平面AA1BB1所成角,解三角形可得答案.
解答:
解:取A1B1的中点D,连接C1D,BD,BC1,

∵正三棱柱ABC-A1B1C1的底面为等边三角形,
故C1D⊥取A1B1,
又∵平面AA1BB1∩平面A1B1C1=A1B1,平面AA1BB1⊥平面A1B1C1,C1D?平面A1B1C1,
∴C1D⊥平面AA1BB1,
故∠C1BD即为直线BC1与平面AA1BB1所成角,
∵棱柱底面边长为2,侧棱长为
,
故BD=2,CD=
,
故tan∠C1BD=
=
,
故选:C.

∵正三棱柱ABC-A1B1C1的底面为等边三角形,
故C1D⊥取A1B1,
又∵平面AA1BB1∩平面A1B1C1=A1B1,平面AA1BB1⊥平面A1B1C1,C1D?平面A1B1C1,
∴C1D⊥平面AA1BB1,
故∠C1BD即为直线BC1与平面AA1BB1所成角,
∵棱柱底面边长为2,侧棱长为
| 3 |
故BD=2,CD=
| 3 |
故tan∠C1BD=
| CD |
| BD |
| ||
| 2 |
故选:C.
点评:本题考查的知识点是直线与平面所成的角,其中得到∠C1BD即为直线BC1与平面AA1BB1所成角,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
的定义域为( )
| ||
| x |
| A、[-1,0) |
| B、(0,+∞) |
| C、[-1,0)∪(0,+∞) |
| D、(-∞,0)∪(0,+∞) |
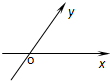 如图,在平面斜坐标系中∠xOy=60°,平面上任意一点P的斜坐标是这样定义的:若
如图,在平面斜坐标系中∠xOy=60°,平面上任意一点P的斜坐标是这样定义的:若| OP |
| e1 |
| e2 |
| e1 |
| e2 |
| A、x2+y2=2 |
| B、x2+y2=4 |
| C、x2+y2+xy=2 |
| D、x2+y2+xy=4 |
点M与点F(3,0)的距离比它到直线x+5=0的距离小2,则点M的轨迹方程为( )
| A、y2=-12x |
| B、y2=6x |
| C、y2=12x |
| D、y2=-6x |