题目内容
解不等式:|2x+1|-|x-4|>3.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:通过讨论x的范围,去掉绝对值解出不等式,从而综合得到答案.
解答:
解:x≥4时,2x+1-x+4>3,解得:x>-2,
-
≤x<4时,2x+1+x-4>3,解得:x>2,
x<-
时,-2x-1+x-4>3,解得:x<-8,
综上:x<-8或x>2.
-
| 1 |
| 2 |
x<-
| 1 |
| 2 |
综上:x<-8或x>2.
点评:本题考查了绝对值不等式的解法,考查了分类讨论思想,是一道基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为
,则直线BC1与平面AA1B1B所成角的正切值为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
点P在直线m上,m在平面a内可表示为( )
| A、P∈m,m∈a |
| B、P∈m,m?a |
| C、P?m,m∈a |
| D、P?m,m?a |
已知函数f(x)的定义域为(-2,2),导函数为f′(x)=x2+2cosx且f(0)=0,则满足f(1+x)+f(x2-x)>0的实数x的取值范围为( )
| A、(-∞,+∞) | ||||
| B、(-1,1) | ||||
C、(-∞,1-
| ||||
D、(-1,1-
|
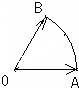 给定两个长度为1的平面向量
给定两个长度为1的平面向量