题目内容

解不等式：（6-2x）（3x+3）＜0．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：把不等式（6-2x）（3x+3）＜0化为（x-3）（x+1）＞0，求出解集即可．
解答： 解：不等式（6-2x）（3x+3）＜0可化为
（x-3）（x+1）＞0，
解得x＜-1或x＞3，
∴原不等式的解集为{x|x＜-1或x＞3}．
点评：本题考查了一元二次不等式的解法与应用问题，是基础题目．
练习册系列答案
相关题目
函数g（x）=log2x，关于方程|g（x）|2+m|g（x）|+2m+3=0在（0，2）内有三个不同的实数解，则实数m的取值范围是（　　）
A、（-∞，4-2
7
）∪（4+2
7
，+∞）
B、（4-2
7
，4+2
7
）
C、（-
3
4
，-
2
3
）
D、（-
3
2
，-
4
3
）
设二次函数f（x）=x2+bx+4，（b∈R）与x轴有交点，若对一切非零实数x，都有f（x+
1
x
）≥0．
（1）求实数b的取值集合；
（2）若b=-4，设函数g（x）=f（x）+
a
f(x)
，x∈[3，2+
2
]，求h（a）=g（x）max-g（x）min的最小值．
设函数f（x）在x0点的某个邻域内有定义，则f（x）在x0处连续的充分必要条件是（　　）
A、
lim
x-x0
 f（x）存在
B、
lim
x→x0-
f（x）=
lim
x→x0+
 f（x）
C、
lim
x-x0
 f（x）=0
D、在x0的某个邻域内，f（x）=f（x0）+α（x），其中
lim
x-x0
 α（x）=0
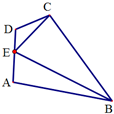如图，在平面四边形ABCD中，DE=1．EC=
7
，∠ADC=
2π
3
∠BEC=
π
3
，求
（1）CD；
（2）求cos∠AEB．
已知△ABC中，a2＞b2+c2，求A的范围．
已知函数f（x）=Asin（2ωx+φ）（其中A＞0，ω＞0，0＜φ＜
π
2
）的周期为π，其图象上一个最高点为M（
π
6
，2）．
（Ⅰ）求f（x）的解析式，并求其单调减区间；
（Ⅱ）当x∈[0，
π
4
]时，求f（x）的最值及相应的x的取值，并求出函数f（x）的值域．
已知等差数列{an}中，a2=2，a4=8，若abn=3n-1，则b2015=
 
．
画出
x
a
一
y
b
=1和
x
b
一
y
a
=1的图象．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网