题目内容
函数g(x)=log2x,关于方程|g(x)|2+m|g(x)|+2m+3=0在(0,2)内有三个不同的实数解,则实数m的取值范围是( )
A、(-∞,4-2
| ||||
B、(4-2
| ||||
C、(-
| ||||
D、(-
|
考点:函数的零点与方程根的关系
专题:计算题,函数的性质及应用
分析:由题意|g(x)|2+m|g(x)|+2m+3=0在(0,2)内有三个不同实数解可化为t2+mt+2m+3=0有两个根,分别在(0,1),[1,+∞)上或在(0,1),{0}上;从而分别讨论即可.
解答:
∵g(x)=log2x在(0,2)上单调递增,
且g(x)<1;
故|g(x)|2+m|g(x)|+2m+3=0在(0,2)内有三个不同实数解可化为
t2+mt+2m+3=0有两个根,分别在(0,1),[1,+∞)上或在(0,1),{0}上;
当若在(0,1),{0}上,则2m+3=0,则m=-
;
故t=0或t=
;
不成立;
若在(0,1),{1}上;
则1+m+2m+3=0,
故m=-
;
故t2+mt+2m+3=0的解为t=
或t=1;成立;
若在(0,1),(1,+∞)上,
则
;
解得-
<m<-
;
故选D.
且g(x)<1;
故|g(x)|2+m|g(x)|+2m+3=0在(0,2)内有三个不同实数解可化为
t2+mt+2m+3=0有两个根,分别在(0,1),[1,+∞)上或在(0,1),{0}上;
当若在(0,1),{0}上,则2m+3=0,则m=-
| 3 |
| 2 |
故t=0或t=
| 3 |
| 2 |
不成立;
若在(0,1),{1}上;
则1+m+2m+3=0,
故m=-
| 4 |
| 3 |
故t2+mt+2m+3=0的解为t=
| 1 |
| 3 |
若在(0,1),(1,+∞)上,
则
|
解得-
| 3 |
| 2 |
| 4 |
| 3 |
故选D.
点评:本题考查了函数的零点与方程的根的关系应用,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
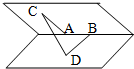 如图在一个二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2
如图在一个二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2| 17 |
| A、30° | B、60° |
| C、90° | D、120° |
已知m,n是两条不同直线,α,β是两个不同的平面,且n?β,则下列叙述正确的是( )
| A、若m∥n,m?α,则α∥β |
| B、若α∥β,m?α,则m∥n |
| C、若m∥n,m⊥α,则α⊥β |
| D、若α∥β,m⊥n,则m⊥α |
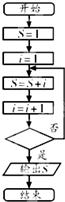 阅读如图所示的程序框图( 框图中的赋值符号“=”也可以写成“←”或“:=”),若输出S的值等于7,那么在程序框图中的判断框内应填写的条件是( )
阅读如图所示的程序框图( 框图中的赋值符号“=”也可以写成“←”或“:=”),若输出S的值等于7,那么在程序框图中的判断框内应填写的条件是( )| A、i>2? | B、i>3? |
| C、i>4? | D、i>5? |
已知直线x-2y-a=0与圆:x2+y2+2x-4y=0相切,则a=( )
| A、0 | B、-10或0 |
| C、-3或0 | D、--10 |