题目内容
若x＞y＞1，且0＜a＜1，则①ax＜ay；②logax＞logay；③x-a＞y-a；④logxa＜logya，其中不成立的个数是 ．
考点：命题的真假判断与应用
专题：不等式的解法及应用,简易逻辑
分析：由x＞y＞1，且0＜a＜1结合幂函数、指数函数、对数函数的性质逐一分析四个命题得答案．
解答：
解：∵0＜a＜1，x＞y＞1，
由指数函数的性质可得①ax＜ay正确；
由对数函数的性质可得②logax＞logay错误；
由幂函数的性质可得③x-a＞y-a错误；
logxa=
，logya=
，
∵lgx＞lgy＞0，
∴
＜
，
又lga＜0，
∴
＞
，命题④错误．
∴命题①正确，②③④错误．
∴不成立命题的个数是3．
故答案为：3．
由指数函数的性质可得①ax＜ay正确；
由对数函数的性质可得②logax＞logay错误；
由幂函数的性质可得③x-a＞y-a错误；
logxa=
| lga |
| lgx |
| lga |
| lgy |
∵lgx＞lgy＞0，
∴
| 1 |
| lgx |
| 1 |
| lgy |
又lga＜0，
∴
| lga |
| lgx |
| lga |
| lgy |
∴命题①正确，②③④错误．
∴不成立命题的个数是3．
故答案为：3．
点评：本题考查了命题的真假判断与应用，考查了基本初等函数的性质，是基础题．
练习册系列答案
相关题目
如图是一个几何体的三视图（单位：cm），计算这个几何体的体积与表面积．若关于x的方程25-|x+1|-4×5-|x+1|=m有实根，则实数m的取值范围是（ ）
| A、m＜0 | B、m≥-4 |
| C、-4≤m＜0 | D、-3≤m＜0 |
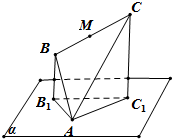如图，边长为4的正△ABC顶点A在平面α上，B，C在平面α的同侧，M为BC的中点．若△ABC在平面α上的射影是以A为直角顶点的三角形AB1C1，则M到平面α的距离的取值范围是已知关于x的不等式
＜1的解集为{x|x＜1或x＞3}，则a的值为（ ）
| ax |
| x-1 |
| A、3 | ||
B、
| ||
C、-
| ||
D、
|