题目内容
用平面α截半径为R的球，截面到球心的距离为
，则截面圆面积为 ．
| R |
| 2 |
考点：球的体积和表面积
专题：空间位置关系与距离
分析：根据球的截面为圆，求出半径即可求出面积．
解答：
解：平面α截半径为R的球，截面为圆，半径r，
∵截面到球心的距离为
，
∴r=
R，
截面圆面积为
，
故答案为：
∵截面到球心的距离为
| R |
| 2 |
∴r=
| ||
| 2 |
截面圆面积为
| 3πR2 |
| 4 |
故答案为：
| 3πR2 |
| 4 |
点评：本题考查了球的几何性质，圆的面积公式，属于容易题．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）在[0，+∞）上可导，其导函数记作f′（x），f（0）=-2，且f（x+π）=
f（x），当x∈[0，π）时，f′（x）•cos2x＞f（x）•sin2x-f′（x），若方程f（x）+knsecx=0在[0，+∞）上有n个解，则数列{
}的前n项和为（ ）
| 1 |
| 2 |
| n |
| k2n |
| A、（n-1）•2n+1 | ||
| B、（n-1）•2n+1+2 | ||
| C、n•2n-1 | ||
D、
|
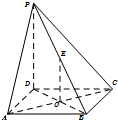如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是正方形，AC与BD交于点O，E为PB的中点．
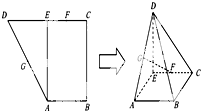如图，已知直角梯形ABCD中，E为CD边中点，且AE⊥CD，又G，F分别为DA，EC的中点，将△ADE沿AE折叠，使得DE⊥EC．