题目内容
已知关于x的不等式
<1的解集为{x|x<1或x>3},则a的值为( )
| ax |
| x-1 |
| A、3 | ||
B、
| ||
C、-
| ||
D、
|
考点:其他不等式的解法
专题:转化思想,不等式的解法及应用
分析:把不等式
<1化为[(a-1)x+1](x-1)<0;由题意得a-1<0,且-
=3,求出a的值.
| ax |
| x-1 |
| 1 |
| a-1 |
解答:
解:不等式
<1可化为
<0,
即[(a-1)x+1](x-1)<0;
且原不等式的解集为{x|x<1或x>3},
∴a-1<0,
∴原不等式可化为(x+
)(x-1)>0,
令-
=3,
解得a=
,
∴a的值为
.
故选:D.
| ax |
| x-1 |
| (a-1)x+1 |
| x-1 |
即[(a-1)x+1](x-1)<0;
且原不等式的解集为{x|x<1或x>3},
∴a-1<0,
∴原不等式可化为(x+
| 1 |
| a-1 |
令-
| 1 |
| a-1 |
解得a=
| 2 |
| 3 |
∴a的值为
| 2 |
| 3 |
故选:D.
点评:本题考查了不等式的解法与应用问题,解题时应把不等式进行转化,是基础题.

练习册系列答案
相关题目
已知三棱锥的三视图如图所示,则它的外接球的表面积为( )


| A、4π | B、8π |
| C、12π | D、16π |
有一个几何体的三视图如图所示,这个几何体应该是一个( )


| A、圆台 | B、圆锥 | C、圆柱 | D、都不对 |
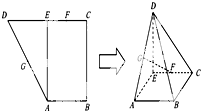 如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.
如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.