题目内容
若关于x的方程25-|x+1|-4×5-|x+1|=m有实根，则实数m的取值范围是（ ）
| A、m＜0 | B、m≥-4 |
| C、-4≤m＜0 | D、-3≤m＜0 |
考点：根的存在性及根的个数判断
专题：计算题,转化思想,函数的性质及应用
分析：本题考查的是根的存在性问题以及根的个数问题．在解答时可以先将t=5-|x+1|看为一个整体，将问题转化为分析方程t2-4t=m有实根时，求m的范围．即可获得问题的解答．
解答：
解：令t=5-|x+1|，
则关于x的方程25-|x+1|-4×5-|x+1|=m有实根即关于t的方程t2-4t=m有实根，
又因为0＜t≤1，
且m=t2-4t=（t-2）2-4，
∴m的范围是[-3，0）．
故选D．
则关于x的方程25-|x+1|-4×5-|x+1|=m有实根即关于t的方程t2-4t=m有实根，
又因为0＜t≤1，
且m=t2-4t=（t-2）2-4，
∴m的范围是[-3，0）．
故选D．
点评：本题考查的是根的存在性问题以及根的个数问题．在解答的过程当中充分体现了问题转化的思想、整体代换的思想以及数形结合的思想．值得同学们体会反思．
练习册系列答案
名校课堂系列答案
相关题目
函数f（x）=
+lg(2-x-1)的定义域为（ ）
| -2 | ||
|
| A、（-5，+∞） |
| B、[-5，+∞） |
| C、（-5，0） |
| D、（-2，0） |
设Sn为数列{an}的前n项和，an=1+2+22+…+2n-1，则Sn的值为（ ）
| A、2n-1 |
| B、2n-1-1 |
| C、2n-n-2 |
| D、2n+1-n-2 |
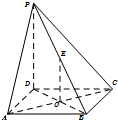如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是正方形，AC与BD交于点O，E为PB的中点．