题目内容
求证:函数f(x)=
(0,+∞)上是减函数,在(-∞,0)上是增函数.
| 1 |
| x2 |
考点:函数单调性的判断与证明
专题:证明题,函数的性质及应用
分析:运用单调性的定义证明,注意作差、变形、定符号和下结论几个步骤.
解答:
证明:设0<m<n,则
f(m)-f(n)=
-
=
由于0<m<n,则n-m>0,n+m>0,mn>0,
则f(m)-f(n)>0,即f(m)>f(n),
则f(x)在(0,+∞)上是减函数;
同理可证,f(x)在(-∞,0)上是增函数.
f(m)-f(n)=
| 1 |
| m2 |
| 1 |
| n2 |
| (n-m)(n+m) |
| m2n2 |
由于0<m<n,则n-m>0,n+m>0,mn>0,
则f(m)-f(n)>0,即f(m)>f(n),
则f(x)在(0,+∞)上是减函数;
同理可证,f(x)在(-∞,0)上是增函数.
点评:本题考查函数的单调性的证明,注意运用定义,考查运算能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=
的定义域为( )
| x2-9 |
| A、[-3,3] |
| B、(-3,3) |
| C、(-∞,-3]∪[3,+∞) |
| D、(-∞,-3)∪(3,+∞) |
若二面角α-L-β的大小为
,此二面角的张口内有一点P到α、β的距离分别为1和2,则P点到棱l的距离是( )
| π |
| 3 |
A、
| ||||
| B、2 | ||||
C、2
| ||||
D、2
|
有一个几何体的三视图如图所示,这个几何体应该是一个( )


| A、圆台 | B、圆锥 | C、圆柱 | D、都不对 |
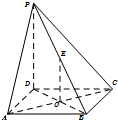 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,AC与BD交于点O,E为PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,AC与BD交于点O,E为PB的中点.