题目内容
若数列{an}为等比数列,an>0,a10a11=e,则lna1+lna2+…+lna20= .
考点:等比数列的性质,对数的运算性质
专题:计算题,等差数列与等比数列
分析:由已知中数列{an}为等比数列,且an>0,根据等比数列的性质,可得a1•a2•…•a20=(a10•a11)10,进而可得lna1+lna2+…+lna20=10ln(a10•a11),结合a10a11=e,可得答案.
解答:
解:若数列{an}为等比数列,且an>0,
∴lna1+lna2+…+lna20=ln(a1•a2•…•a20)=ln(a10•a11)10=10ln(a10•a11)
∵a10a11=e,
∴lna1+lna2+…+lna20=10
故答案为:10.
∴lna1+lna2+…+lna20=ln(a1•a2•…•a20)=ln(a10•a11)10=10ln(a10•a11)
∵a10a11=e,
∴lna1+lna2+…+lna20=10
故答案为:10.
点评:本题考查的知识点是等比数列的性质,对数的运算性质,其中根据等比数列的性质得到a1•a2•…•a20=(a10•a11)10,是解答的关键.

练习册系列答案
相关题目
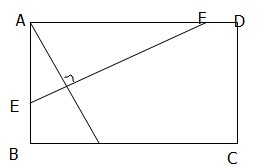 如图所示,已知正方形ABCD的边长为32cm,点P在BC上,且BP=16cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长.
如图所示,已知正方形ABCD的边长为32cm,点P在BC上,且BP=16cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长. 把地球看作半径为R的球,地球上的A、B两地都在北纬45°上,A、B两地的球面距离为
把地球看作半径为R的球,地球上的A、B两地都在北纬45°上,A、B两地的球面距离为