题目内容
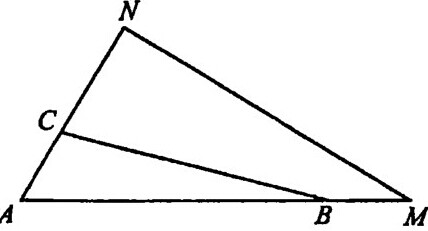
如图，在△ABC中，AB=4，AC=1，∠BAC=60°．求BC的长和△ABC的面积；
考点：正弦定理,余弦定理
专题：解三角形
分析：在三角形ABC中，由AB，AC，以及cos∠BAC的值，利用余弦定理求出BC的长，再利用三角形面积公式即可求出三角形ABC面积．
解答：
解：∵在△ABC中，AB=4，AC=1，∠BAC=60°，
∴由余弦定理得：BC2=AC2+AB2-2AC•ABcos∠BAC=1+16-4=13，即BC=
，
由三角形面积公式得：S△ABC=
AC•ABsin∠BAC=
×1×4×
=
．
∴由余弦定理得：BC2=AC2+AB2-2AC•ABcos∠BAC=1+16-4=13，即BC=
| 13 |
由三角形面积公式得：S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评：此题考查了余弦定理，三角形面积公式，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
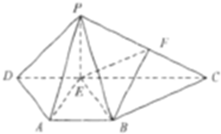如图，在四棱维P-ABCD中，侧面PCD⊥底面ABCD．四边形ABCD是等腰梯形．AB∥CD．∠ADC=∠PDC=
将形如