题目内容
对任意x∈R，函数f（x）满足f（x+1）=
+1，设an=[f（n）]2-2f（n），数列{an}的前2013项和为-1003，则f（2013）= ．
| 2f(x)-[f(x)]2 |
考点：数列的求和
专题：综合题,函数的性质及应用,等差数列与等比数列
分析：f（x+1）=
+1可变形为[f（x+1）]2-2f（x+1）+1=2f（x）-[f（x）]2，从而an+1+an=-1，再由数列{an}的前2013项和为-1003可求a2013=3，则[f（2013）]2-2f（2013）=3，
由此可求答案，注意判断f（2013）的范围．
| 2f(x)-[f(x)]2 |
由此可求答案，注意判断f（2013）的范围．
解答：
解：∵f（x+1）=
+1，
∴f（x+1）-1=
，
两边平方得：[f（x+1）-1]2=2f（x）-f（x）2
⇒[f（x+1）]2-2f（x+1）+1=2f（x）-[f（x）]2，
即an+1+an=-1，即数列{an}任意相邻两项相加为常数-1，
则S2013=1006×（-1）+a2013=-1003⇒a2013=3，
∴[f（2013）]2-2f（2013）=3，
解得f（2013）=3或-1，
又由f（x+1）=
+1，可得f（x+1）≥1，
可得f（2013）=3．
故答案为：3．
| 2f(x)-[f(x)]2 |
∴f（x+1）-1=
| 2f(x)-[f(x)]2 |
两边平方得：[f（x+1）-1]2=2f（x）-f（x）2
⇒[f（x+1）]2-2f（x+1）+1=2f（x）-[f（x）]2，
即an+1+an=-1，即数列{an}任意相邻两项相加为常数-1，
则S2013=1006×（-1）+a2013=-1003⇒a2013=3，
∴[f（2013）]2-2f（2013）=3，
解得f（2013）=3或-1，
又由f（x+1）=
| 2f(x)-[f(x)]2 |
可得f（2013）=3．
故答案为：3．
点评：该题为数列与函数的综合题，利用函数的性质推得数列递推式是解决该题的关键，本题容易忽略对f（2013）范围的判断．
练习册系列答案
相关题目
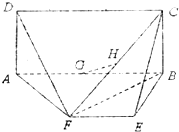已知矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直，AB∥FE，G、H分别为AB、CF的中点，AB=2，AD=EF=1，∠AFB=