题目内容
设F1,F2为椭圆C1:
+
=1(a>b>0)与双曲线C2的公共点左右焦点,它们在第一象限内交于点M,
△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2.若椭圆C1的离心率e=
,则双曲线C2的离心率是 .
| x2 |
| a2 |
| y2 |
| b2 |
△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2.若椭圆C1的离心率e=
| 3 |
| 8 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由已知条件推导出|MF2|=|F1F2|=2c,
=
,由此能求出双曲线C2的离心率.
| 2c |
| 2+2c |
| 3 |
| 8 |
解答:
 解:∵F1,F2为椭圆C1:
解:∵F1,F2为椭圆C1:
+
=1(a>b>0)与双曲线C2的公共点左右焦点,
△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2,
∴|MF2|=|F1F2|=2c,
∵椭圆C1的离心率e=
,
∴
=
,解得c=
,
∴双曲线C2的离心率e=
=
.
故答案为:
.
 解:∵F1,F2为椭圆C1:
解:∵F1,F2为椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2,
∴|MF2|=|F1F2|=2c,
∵椭圆C1的离心率e=
| 3 |
| 8 |
∴
| 2c |
| 2+2c |
| 3 |
| 8 |
| 3 |
| 5 |
∴双曲线C2的离心率e=
2×
| ||
2-2×
|
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,注意双曲线、椭圆性质的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
方程x2-4|x|-3=m有四个解的m的取值范围是( )
| A、(-7,-3) |
| B、(0,7) |
| C、[0,7) |
| D、[-7,-3) |
y=sin(2x-
)-sin2x的一个单调递增区间是( )
| π |
| 3 |
A、[-
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知空间四点A(4,1,3),B(2,3,1),C(3,7,-5),D(x,-1,3)共面,则x=( )
| A、4 | B、1 | C、10 | D、11 |
“B=60°”是“△ABC三个内角成等差数列”的( )
| A、充分非必要条件 |
| B、充要条件 |
| C、必要非充分条件 |
| D、既不充分又非必要条件. |
如图,已知AB⊥平面BCD,BC⊥CD,则图中直角三角形的个数为( )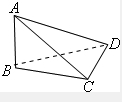

| A、1 | B、2 | C、3 | D、4 |
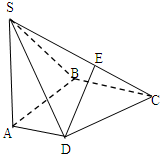 四棱锥S-ABCD中,底面ABCD为直角梯形,AB垂直于AD和BC,SA⊥面ABCD,SA=AB=BC=2,AD=1.求:
四棱锥S-ABCD中,底面ABCD为直角梯形,AB垂直于AD和BC,SA⊥面ABCD,SA=AB=BC=2,AD=1.求: