Question

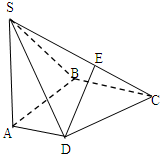四棱锥S-ABCD中，底面ABCD为直角梯形，AB垂直于AD和BC，SA⊥面ABCD，SA=AB=BC=2，AD=1．求：
（1）V_S-ABCD；
（2）SC上是否存在点E，使DE⊥SB？若存在，确定点E的位置．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（1）由已知得V_S-ABCD=

1

3

Sh=

1

3

SA×（AD+BC）•AB•

1

2

，由此能求出结果．
（2）以A为原点，AD为x轴，AB为y轴，AS为z轴，建立空间直角坐标系，利用向量法求出当E为SC中点时，DE⊥SB．

解答： 解：（1）∵四棱锥S-ABCD中，底面ABCD为直角梯形，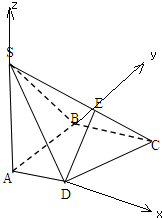
AB垂直于AD和BC，SA⊥面ABCD，SA=AB=BC=2，AD=1，
∴V_S-ABCD=

1

3

Sh=

1

3

SA×（AD+BC）•AB•

1

2

=

1

6

×2×（1+2）×2
=2．
（2）以A为原点，AD为x轴，AB为y轴，AS为z轴，
建立空间直角坐标系，
由题意知D（1，0，0），S（0，0，2），C（2，2，0），
B（0，2，0），设

CE

=λ

CS

=（-2λ，-2λ，2λ），
设E（a，b，c），

CE

=（a-2，b-2，c），
则

a=2-2λ b=2-2λ c=2λ

，∴E（2-2λ，2-2λ，2λ），

DE

=（1-2λ，2-2λ，2λ），

SB

=（0，2，-2），
∵DE⊥SB，
∴

DE

•

SB

=2（2-2λ）-2×2λ=0，解得λ=

1

2

，
∴当E为SC中点时，DE⊥SB．

点评：本题考查四棱锥的体积的求法，考查满足异面直线垂直的点的位置的确定，解题时要注意向量法的合理运用．