题目内容
如图，已知AB⊥平面BCD，BC⊥CD，则图中直角三角形的个数为（ ）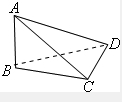
| A、1 | B、2 | C、3 | D、4 |
考点：直线与平面垂直的性质
专题：计算题,空间位置关系与距离
分析：由线面垂直的性质和判定定理，通过一一列举，即可推出有4个直角三角形．
解答：
解：由于AB⊥平面BCD，
则AB⊥BC，AB⊥BD，AB⊥CD，
又BC⊥CD，
则CD⊥平面ABC，
则CD⊥AC，
故△ABC，△ACD，△ABD，△BCD均为直角三角形．
故选D．
解：由于AB⊥平面BCD，则AB⊥BC，AB⊥BD，AB⊥CD，
又BC⊥CD，
则CD⊥平面ABC，
则CD⊥AC，
故△ABC，△ACD，△ABD，△BCD均为直角三角形．
故选D．
点评：本题考查直线与平面垂直的判定和性质，考查推理能力，属于基础题．
练习册系列答案
相关题目
已知z1，z2∈C，设A：z12+z22=0，B：z1，z2全为零，则A是B的（ ）
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知椭圆
+
=1上一点P到它的右准线的距离为10，则点P到它的左焦点的距离是（ ）
| x2 |
| 100 |
| y2 |
| 36 |
| A、8 | B、10 | C、12 | D、14 |