题目内容
函数f(x)=
,则
f(x)dx的值为( )
|
| ∫ | 2 -2 |
| A、π+6 | B、π-2 | C、2π | D、8 |
考点:定积分
专题:导数的概念及应用
分析:先根据定积分的几何意义,将原式化成:∫-20(2-x)dx+∫02
dx,再利用定积分的运算法则,找出被积函数的原函数,进行计算即可
| 4-x2 |
解答:
解:
f(x)dx=(∫-20(2-x)dx+∫02
dx)
∵∫-20(2-x)dx=(2x-
x2)|-20=6,
∵∫02
dx表示的几何意义是以原点为圆心,以2为半径的圆的面积的四分之一,
∴∫02
dx=
π×22=π
∴
-22f(x)dx=∫-20(2-x)dx+∫02
dx=π+6
故选:A.
| ∫ | 2 -2 |
| 4-x2 |
∵∫-20(2-x)dx=(2x-
| 1 |
| 2 |
∵∫02
| 4-x2 |
∴∫02
| 4-x2 |
| 1 |
| 4 |
∴
| ∫ | 2 -2 |
| 4-x2 |
故选:A.
点评:本题主要考查定积分的基本运算,解题关键是找出被积函数的原函数,利用定积分的几何意义,本题属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
+
的两个极值点分别为x1,x2,且x1∈(0,1),x2∈(1,+∞),点P(m,n)表示的平面区域为D,若函数y=loga(x+4)(a>1)的图象上存在区域D内的点,则实数a的取值范围为( )
| x3 |
| 3 |
| mx2+(m+n)x+1 |
| 2 |
| A、(1,3] |
| B、(1,3) |
| C、(3,+∞) |
| D、[3,+∞) |
函数f(x)=4lnx-x2的大致图象是( )
A、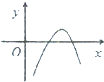 |
B、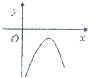 |
C、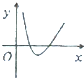 |
D、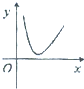 |