题目内容
已知某几何体的三视图如图所示,则该几何体的体积是( )


| A、1440 | B、1200 |
| C、960 | D、720 |
考点:由三视图求面积、体积
专题:计算题
分析:由三视图可知:该几何体是一个棱长分别为20,8,9,砍去一个角的一个三棱锥(长方体的一个角).据此即可得出体积.
解答:
 解:由三视图可知:该几何体是一个棱长分别为20,8,8,砍去一个三棱锥(长方体的一个角)的几何体.如图:
解:由三视图可知:该几何体是一个棱长分别为20,8,8,砍去一个三棱锥(长方体的一个角)的几何体.如图:
∴该几何体的体积V=20×9×8-
×
×9×8×20=1200.
故选:B.
 解:由三视图可知:该几何体是一个棱长分别为20,8,8,砍去一个三棱锥(长方体的一个角)的几何体.如图:
解:由三视图可知:该几何体是一个棱长分别为20,8,8,砍去一个三棱锥(长方体的一个角)的几何体.如图:∴该几何体的体积V=20×9×8-
| 1 |
| 3 |
| 1 |
| 2 |
故选:B.
点评:本题考查空间几何体的三视图的应用,由三视图正确恢复原几何体是解题的关键.

练习册系列答案
相关题目
函数f(x)=log2(4x-x2)的单调递减区间是( )
| A、(0,4) |
| B、(0,2] |
| C、[2,4) |
| D、(2,+∞) |
若偶函数f(x)在(-∞,-1]上是增函数,则下列关系式中成立的是( )
A、f(-
| ||
B、f(π)<f(-
| ||
C、f(π)<f(-1)<f(-
| ||
D、f(-1)<f(-
|
已知一个三角形的三边长分别是5,5,6,一只蚂蚁在其内部爬行,若不考虑蚂蚁的大小,则某时刻该蚂蚁距离三角形的三个顶点的距离均超过2的概率是( )
A、2-
| ||
B、1-
| ||
C、2-
| ||
D、1-
|
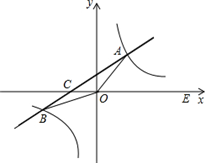 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=