Question

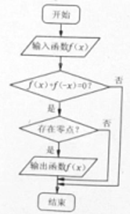
某流程图如图所示，现输入下列4个函数，则可以输出的函数是（　　）

• A、f（x）=

  |x|

  x

• B、f（x）=

  cosx

  x

  （-

  π

  2

  ＜x＜

  π

  2

  ，且x≠0）
• C、f（x）=

  2′-1

  2′+1

• D、f（x）=x²ln（x²+1）

Answer 1

考点：程序框图

专题：算法和程序框图

分析：本题的框图是一个选择结构，其算法是找出存在零点的奇函数，由此规则对四个选项进行比对，即可得出正确选项．

解答： 解：由框图知，其算法是输出存在零点的奇函数，
A中，函数f（x）=

. x .

2

不能输出，因为此函数不是奇函数；A不正确．
B中，函数f（x）=

cosx

x

（-

π

2

＜x＜

π

2

，且x≠0）不能输出，因为此函数不存在零点；B不正确．
C中，函数f（x）=

2x-1

2x+1

能输出，因为f（-x）=

2-x-1

2-x+1

=

1-2-x

1+2-x

=-f（x），
即（x）=

2x-1

2x+1

为奇函数，又f（1）=0，即函数存在零点；C正确．
D中，函数f（x）=x²ln（x²+1）不能输出，因为它是偶函数，不是奇函数；D不正确．
故选：C．

点评：本题考查选择结构，解答本题的关键是根据框图得出函数所满足的性质，然后比对四个选项中的函数，对四个函数的性质比较了解也是判断出正确答案的关键．