题目内容
数列
,
,
,
,
,…的一个通项公式为 .
| 15 |
| 2 |
| 24 |
| 5 |
| 35 |
| 10 |
| 48 |
| 17 |
| 63 |
| 26 |
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:由数列{an}:
,
,
,
,
,…,可知:分子为(n+3)2-1,分母:变形为12+1,22+1,32+1,42+1,52+1,…,即可得出.
| 15 |
| 2 |
| 24 |
| 5 |
| 35 |
| 10 |
| 48 |
| 17 |
| 63 |
| 26 |
解答:
解:由数列{an}:
,
,
,
,
,…,可知:分子为(n+3)2-1,分母:变形为12+1,22+1,32+1,42+1,52+1,…,
可得一个通项公式为:an=
,
故答案为:an=
.
| 15 |
| 2 |
| 24 |
| 5 |
| 35 |
| 10 |
| 48 |
| 17 |
| 63 |
| 26 |
可得一个通项公式为:an=
| (n+3)2-1 |
| n2+1 |
故答案为:an=
| (n+3)2-1 |
| n2+1 |
点评:本题考查了通过观察分析猜想归纳求数列的通项公式,属于基础题.

练习册系列答案
相关题目
若点P(a,b)与Q(b-1,a+1)(a≠b-1)关于直线l对称,则直线l的方程是( )
| A、x+y=0 |
| B、x-y=0 |
| C、x+y-1=0 |
| D、x-y+1=0 |
设O是△ABC的三边中垂线的交点,a,b,c分别为角A,B,C对应的边,已知b2-2b+c2=0,则
•
的范围是( )
| BC |
| AO |
| A、[0,+∞) | ||
| B、[0,2) | ||
C、[-
| ||
D、[-
|
已知点 M(x,y)的坐标满足
,N点的坐标为(1,-3),点 O为坐标原点,则
•
的最小值是( )
|
| ON |
| OM |
| A、12 | B、5 | C、-6 | D、-21 |
已知函数f(x)=
,若函数g(x)=f(x)+x+a在R上恰有两个相异零点,则实数a的取值范围为( )
|
| A、[-1,+∞) |
| B、(-1,+∞) |
| C、(-∞,0) |
| D、(-∞,1] |
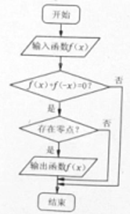
某流程图如图所示,现输入下列4个函数,则可以输出的函数是( )

A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
| D、f(x)=x2ln(x2+1) |
已知向量
=(m,2),向量
=(2,-3),若
⊥
,则实数m的值是( )
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、3 | ||
C、
| ||
| D、-3 |