题目内容
有6个人,每个人都以相同的概率被分配到4间房中的每一间中,某指定房间中恰有2人的概率为 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:从6个人中任意选出2个人,放到某个房间中有C62种不同的方法,其余的4个人任意住到剩余的3个房间内,
有34种方法,故指定的某个房间中有2人的宿方法有 C62•34 种,由此求得指定的某个房间中有2人的概率.
有34种方法,故指定的某个房间中有2人的宿方法有 C62•34 种,由此求得指定的某个房间中有2人的概率.
解答:
解:从6个人中任意选出2个人,放到某个房间中有C62种不同的方法,
其余的4个人任意住到剩余的3个房间内,有34种方法,
故指定的某个房间中有2人的宿方法有 C62•34 种,
∴指定的某个房间中有2人的概率P=
=
.
故答案为:
.
其余的4个人任意住到剩余的3个房间内,有34种方法,
故指定的某个房间中有2人的宿方法有 C62•34 种,
∴指定的某个房间中有2人的概率P=
| ||
| 46 |
| 1215 |
| 4096 |
故答案为:
| 1215 |
| 4096 |
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
设O是△ABC的三边中垂线的交点,a,b,c分别为角A,B,C对应的边,已知b2-2b+c2=0,则
•
的范围是( )
| BC |
| AO |
| A、[0,+∞) | ||
| B、[0,2) | ||
C、[-
| ||
D、[-
|
已知函数f(x)=
,若函数g(x)=f(x)+x+a在R上恰有两个相异零点,则实数a的取值范围为( )
|
| A、[-1,+∞) |
| B、(-1,+∞) |
| C、(-∞,0) |
| D、(-∞,1] |
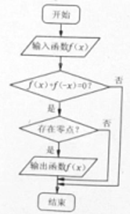
某流程图如图所示,现输入下列4个函数,则可以输出的函数是( )

A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
| D、f(x)=x2ln(x2+1) |
已知函数f(x)=x3-f′(-1)x2-x,则f′(1)等于( )
A、
| ||
B、-
| ||
| C、6 | ||
| D、-6 |