题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,且与抛物线y2=x交于A、B两点,若△OAB(O为坐标原点)的面积为2
,则椭圆C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知得
,由此能求出椭圆C的方程.
|
解答:
解:∵椭圆C:
+
=1(a>b>0)与抛物线y2=x交于A、B两点,
△OAB(O为坐标原点)的面积为2
,
∴设A(x,
),B(x,-
),x
=2
,解得x=2,
由已知得
,解得a=2
,b=2,
∴椭圆C的方程为
+
=1.
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
△OAB(O为坐标原点)的面积为2
| 2 |
∴设A(x,
| x |
| x |
| x |
| 2 |
由已知得
|
| 2 |
∴椭圆C的方程为
| x2 |
| 8 |
| y2 |
| 4 |
故选:A.
点评:本题考查椭圆方程的求法,是基础题,解题时要认真审题,注意椭圆的简单性质的合理运用.

练习册系列答案
相关题目
已知函数f(x)=
,若函数g(x)=f(x)+x+a在R上恰有两个相异零点,则实数a的取值范围为( )
|
| A、[-1,+∞) |
| B、(-1,+∞) |
| C、(-∞,0) |
| D、(-∞,1] |
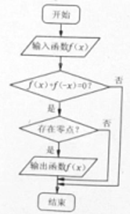
某流程图如图所示,现输入下列4个函数,则可以输出的函数是( )

A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
| D、f(x)=x2ln(x2+1) |
已知函数f(x)=x3-f′(-1)x2-x,则f′(1)等于( )
A、
| ||
B、-
| ||
| C、6 | ||
| D、-6 |
已知向量
=(m,2),向量
=(2,-3),若
⊥
,则实数m的值是( )
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、3 | ||
C、
| ||
| D、-3 |