题目内容
正数列{an}和{bn}对任意n∈N+,an,bn,an+1成等差数列,且an+1=
,判断数列{
}是否为等差数列.
| bnbn+1 |
| bn |
考点:等差关系的确定
专题:等差数列与等比数列
分析:由an,bn,an+1成等差数列,得2bn=an+an+1,结合an+1=
得到2bn=
+
,两边同时除以
得答案.
| bnbn+1 |
| bn-1bn |
| bnbn+1 |
| bn |
解答:
解:由an,bn,an+1成等差数列,得2bn=an+an+1,
又an+1=
,得对任意n≥2,n∈N*,有2bn=
+
.
即2
=
+
.
∴{
}是等差数列.
又an+1=
| bnbn+1 |
| bn-1bn |
| bnbn+1 |
即2
| bn |
| bn-1 |
| bn+1 |
∴{
| bn |
点评:本题考查了等差关系的确定,考查了等差数列和等比数列的性质,是基础题.

练习册系列答案
相关题目
执行如图所示的程序框图,若m=4,则输出的结果为( )
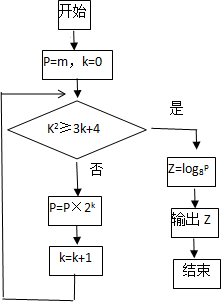

| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
已知点 M(x,y)的坐标满足
,N点的坐标为(1,-3),点 O为坐标原点,则
•
的最小值是( )
|
| ON |
| OM |
| A、12 | B、5 | C、-6 | D、-21 |
已知函数f(x)=
,若函数g(x)=f(x)+x+a在R上恰有两个相异零点,则实数a的取值范围为( )
|
| A、[-1,+∞) |
| B、(-1,+∞) |
| C、(-∞,0) |
| D、(-∞,1] |
某流程图如图所示,现输入下列4个函数,则可以输出的函数是( )
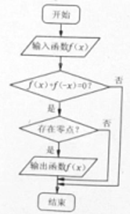

A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
| D、f(x)=x2ln(x2+1) |
已知i是虚数单位,若z1=1+i,z2=1-i,(m∈R),则
的虚部为( )
| z1 |
| z2 |
| A、-1 | B、1 | C、i | D、-i |