题目内容

已知直线直线l1：a1x+b1y+c1=0直线l2：a2x+b2y+c2=0相交，证明方程：a1x+b1y+c1+λ（a2x+b2y+c2）=0（λ∈R）表示过l1与l2交点的直线．
考点：两条直线的交点坐标
专题：直线与圆
分析：假设P（x0，y0）为直线l1，l2的交点，可得a1x0+b1y0+c1+1=0直线l2：a2x0+b2y0+c2=0，可得a1x0+b1y0+c1+λ（a2x0+b2y0+c2）=0，即可证明．
解答： 证明：假设P（x0，y0）为直线l1，l2的交点，
∴a1x0+b1y0+c1=0直线l2：a2x0+b2y0+c2=0，
∴a1x0+b1y0+c1+λ（a2x0+b2y0+c2）=0，
∴a1x+b1y+c1+λ（a2x+b2y+c2）=0（λ∈R）表示过l1与l2交点的直线．
点评：本题考查了直线的交点、直线系，考查了计算能力，属于基础题．
练习册系列答案
相关题目
写出下列数列的一个通项公式：（可以不写过程）
（1）3，5，9，17，33，…；
（2）
2
3
，
4
15
，
6
35
，
8
63
，…；
（3）1，0，-
1
3
，0，
1
5
，0，-
1
7
，0，…．
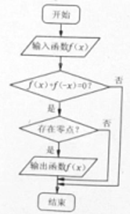
某流程图如图所示，现输入下列4个函数，则可以输出的函数是（　　）
A、f（x）=
|x|
x
B、f（x）=
cosx
x
（-
π
2
＜x＜
π
2
，且x≠0）
C、f（x）=
2′-1
2′+1
D、f（x）=x2ln（x2+1）
已知y=
x
x
，则y′=
 
．
根据下列条件，求相应的等差数列{an}的有关求和数
（1）a1=20，an=54，Sn=999，求d及n
（2）d=
1
3
，n=37，Sn=629，求a1及an
（3）a1=
5
6
，d=-
1
6
，Sn=-5，求n及an
（4）d=12，n=15，an=-10，求a1及Sn．
下列结论中正确的是（　　）
A、Z⊆N⊆Q⊆R⊆C
B、N⊆Z⊆Q⊆C⊆R
C、N⊆Z⊆Q⊆R⊆C
D、R⊆N⊆Z⊆Q⊆C
已知向量
a
=（m，2），向量
b
=（2，-3），若
a
⊥
b
，则实数m的值是（　　）
A、-2
B、3
C、
4
3
D、-3
已知i是虚数单位，若z1=1+i，z2=1-i，（m∈R），则
z1
z2
的虚部为（　　）
A、-1B、1C、iD、-i
某电视台的一个综艺栏目对六个不同的节目排演出顺序，最前只能排甲或乙，最后不能排甲，则不同的排法共有（　　）
A、192种B、216种
C、240种D、288种

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网