题目内容
已知函数f(x)=alnx-
,其中a≥0
(Ⅰ)当a=1时,求曲线y=f(x)在(1,f(1))处的切线方程;
(Ⅱ)讨论f(x)在其定义域上的单调性.
| (a+1)x |
| x+1 |
(Ⅰ)当a=1时,求曲线y=f(x)在(1,f(1))处的切线方程;
(Ⅱ)讨论f(x)在其定义域上的单调性.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)当a=1时,f(x)=lnx-
求出函数的导数,求出切线的斜率,可得切线方程.
(Ⅱ)求出函数f(x)的定义域为(0,+∞),求出函数的导数,通过①当a=0时,②当a>0时,构造g(x)=ax2+(a-1)x+a(x∈(0,+∞)),利用△的符号推出a的范围,得到函数的单调区间.
| 2x |
| x+1 |
(Ⅱ)求出函数f(x)的定义域为(0,+∞),求出函数的导数,通过①当a=0时,②当a>0时,构造g(x)=ax2+(a-1)x+a(x∈(0,+∞)),利用△的符号推出a的范围,得到函数的单调区间.
解答:
解:(Ⅰ)当a=1时,f(x)=lnx-
,f/(x)=
-
=
-
…(2分)
∴f/(1)=1-
=
,又f(1)=-1∴切线方程为y-(-1)=
(x-1),
即y=
x-
…(5分)
(Ⅱ)f(x)的定义域为(0,+∞),
f/(x)=
-
=
…(6分)
①当a=0时,f/(x)=-
=-
<0,
∴f(x)在(0,+∞)上单调递减 …(7分)
②当a>0时,设g(x)=ax2+(a-1)x+a(x∈(0,+∞))
(a)当△=(a-1)2-4a2=-3a2-2a+1≤0,
即a≥
时,f′(x)≥0,∴f(x)在(0,+∞)上单调递增 …(9分)
(b)当△=-3a2-2a+1>0即0<a<
时,由g(x)=0得x=
,
∵(1-a)2-(-3a2-2a+1)=4a2>0,
∴0<x1=
<x2=
,
∴当x∈(0,x1)和(x2,+∞)时,f′(x)≥0,
当x∈(x1,x2)时,f′(x)<0,
∴f(x)单调递增区间为(0,x1)和(x2,+∞),
f(x)单调递减区间为(x1,x2)…(12分)
综上,当a=0时,f(x)单调递减区间为(0,+∞);
当0<a<
时,f(x)单调递增区间为(0,x1)和(x2,+∞),单调递减区间为(x1,x2);
当a≥
时,f(x)单调递增区间为(0,+∞)…(13分)
| 2x |
| x+1 |
| 1 |
| x |
| 2(x+1)-2x |
| (x+1)2 |
| 1 |
| x |
| 2 |
| (x+1)2 |
∴f/(1)=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即y=
| 1 |
| 2 |
| 3 |
| 2 |
(Ⅱ)f(x)的定义域为(0,+∞),
f/(x)=
| a |
| x |
| (a+1)(x+1)-(a+1)x |
| (x+1)2 |
| ax2+(a-1)x+a |
| x(x+1)2 |
①当a=0时,f/(x)=-
| x |
| x(x+1)2 |
| 1 |
| (x+1)2 |
∴f(x)在(0,+∞)上单调递减 …(7分)
②当a>0时,设g(x)=ax2+(a-1)x+a(x∈(0,+∞))
(a)当△=(a-1)2-4a2=-3a2-2a+1≤0,
即a≥
| 1 |
| 3 |
(b)当△=-3a2-2a+1>0即0<a<
| 1 |
| 3 |
1-a±
| ||
| 2a |
∵(1-a)2-(-3a2-2a+1)=4a2>0,
∴0<x1=
1-a-
| ||
| 2a |
1-a+
| ||
| 2a |
∴当x∈(0,x1)和(x2,+∞)时,f′(x)≥0,
当x∈(x1,x2)时,f′(x)<0,
∴f(x)单调递增区间为(0,x1)和(x2,+∞),
f(x)单调递减区间为(x1,x2)…(12分)
综上,当a=0时,f(x)单调递减区间为(0,+∞);
当0<a<
| 1 |
| 3 |
当a≥
| 1 |
| 3 |
点评:本题考查函数的导数的应用,切线方程的求法,函数的单调区间的求法,考查分类讨论以及构造法的应用,考查分析问题解决问题的能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
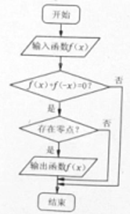
某流程图如图所示,现输入下列4个函数,则可以输出的函数是( )

A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
| D、f(x)=x2ln(x2+1) |
已知向量
=(m,2),向量
=(2,-3),若
⊥
,则实数m的值是( )
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、3 | ||
C、
| ||
| D、-3 |
已知i是虚数单位,若z1=1+i,z2=1-i,(m∈R),则
的虚部为( )
| z1 |
| z2 |
| A、-1 | B、1 | C、i | D、-i |
从正方形的四个顶点及其中心这五个点中,任取两个点,则这两个点的距离不大于该正方形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某电视台的一个综艺栏目对六个不同的节目排演出顺序,最前只能排甲或乙,最后不能排甲,则不同的排法共有( )
| A、192种 | B、216种 |
| C、240种 | D、288种 |
执行如图所示程序框图的算法,输出的结果为( )


| A、log910 |
| B、lg11 |
| C、2 |
| D、log310 |