题目内容
已知正项等比数列{an}满足2a7=3a6+2a5,若存在两项am,an使得
=4a1,则m+n的值为 .
| aman |
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:由等比数列的通项公式结合已知列式求出公比,代入
=4a1,借助于有理指数幂的运算性质求得m+n的值.
| aman |
解答:
解:在正项等比数列{an}中,由2a7=3a6+2a5,得2a1q6=3a1q5+2a1q4,
即2q2=3q+2,解得q=2,
由
=4a1,得
=4a1,
∴2
=4,解得m+n=6.
故答案为:6.
即2q2=3q+2,解得q=2,
由
| aman |
| a12m-1•a12n-1 |
∴2
| m+n-2 |
| 2 |
故答案为:6.
点评:本题考查了等比数列的性质,考查了等比数列的通项公式,是基础的计算题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知点 M(x,y)的坐标满足
,N点的坐标为(1,-3),点 O为坐标原点,则
•
的最小值是( )
|
| ON |
| OM |
| A、12 | B、5 | C、-6 | D、-21 |
某流程图如图所示,现输入下列4个函数,则可以输出的函数是( )
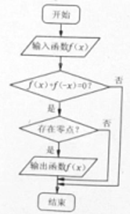

A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
| D、f(x)=x2ln(x2+1) |
下列结论中正确的是( )
| A、Z⊆N⊆Q⊆R⊆C |
| B、N⊆Z⊆Q⊆C⊆R |
| C、N⊆Z⊆Q⊆R⊆C |
| D、R⊆N⊆Z⊆Q⊆C |
从正方形的四个顶点及其中心这五个点中,任取两个点,则这两个点的距离不大于该正方形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|




