题目内容
已知a＞0，b＞0，c＞0，a2b+b2c+c2a=1，则abc（abc-2）的最小值为 ．
考点：二维形式的柯西不等式
专题：计算题,不等式的解法及应用
分析：利用基本不等式求出0＜abc≤
，再换元，利用配方法，即可得出结论．
| 1 |
| 3 |
解答：
解：∵a＞0，b＞0，c＞0，a2b+b2c+c2a=1，
∴1≥3
，
∴0＜abc≤
，
设t=abc，则0＜t≤
，
abc（abc-2）=t（t-2）=（t-1）2-1，
∴t=
时，abc（abc-2）的最小值为-
，
故答案为：-
∴1≥3
| 3 | a3b3c3 |
∴0＜abc≤
| 1 |
| 3 |
设t=abc，则0＜t≤
| 1 |
| 3 |
abc（abc-2）=t（t-2）=（t-1）2-1，
∴t=
| 1 |
| 3 |
| 5 |
| 9 |
故答案为：-
| 5 |
| 9 |
点评：本题考查最值，考查基本不等式的运用，考查配方法，确定0＜abc≤
是关键．
| 1 |
| 3 |
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
一个四面体的顶点都在球面上，它们的正视图、侧视图、俯视图都是右图．图中圆内有一个以圆心为中心边长为1的正方形．则这个四面体的外接球的表面积是（ ）若点P（a，b）与Q（b-1，a+1）（a≠b-1）关于直线l对称，则直线l的方程是（ ）
| A、x+y=0 |
| B、x-y=0 |
| C、x+y-1=0 |
| D、x-y+1=0 |
执行如图所示的程序框图，若m=4，则输出的结果为（ ）
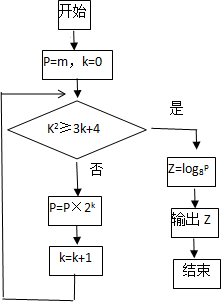
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
某流程图如图所示，现输入下列4个函数，则可以输出的函数是（ ）
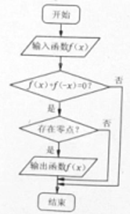
A、f（x）=
| ||||||
B、f（x）=
| ||||||
C、f（x）=
| ||||||
| D、f（x）=x2ln（x2+1） |