题目内容
在运用计算机(器)作函数图象时,经常用到“符号函数”S(x)=
例如要表示分段函数g(x)=
,可以将g(x)表示为g(x)=x•S(x-2)+(-x)•S(2-x)输入计算机,则计算机就会画出函数g(x)的图象.设f(x)=(-x2+4x-3)•S(x-1)+(x2-1)•S(1-x)(x≠1).
(1)请把函数y=f(x)写成分段函数的形式;
(2)画出函数y=f(x)的大致图象;
(3)设F(x)=f(x+k),是否存在实数k,使得F(x)为奇函数?若存在,写出满足条件的k值;若不存在,说明理由.
|
|
(1)请把函数y=f(x)写成分段函数的形式;
(2)画出函数y=f(x)的大致图象;
(3)设F(x)=f(x+k),是否存在实数k,使得F(x)为奇函数?若存在,写出满足条件的k值;若不存在,说明理由.
考点:分段函数的应用
专题:函数的性质及应用
分析:(1)分当x>1、当x=1和当x<1时3种情况加以讨论,分别根据S(x)的对应法则代入,可得f(x)相应范围内的表达式,最后综合可得函数f(x)写成分段函数的形式;
(2)画分段函数每一段的图象即可;
(3)根据第(2)问画的图象,结合函数图象的平移知识,使图象关于原点对称,即可得到奇函数.
(2)画分段函数每一段的图象即可;
(3)根据第(2)问画的图象,结合函数图象的平移知识,使图象关于原点对称,即可得到奇函数.
解答:
解:(Ⅰ)分情况讨论:
①当x>1时,S(x-1)=1且S(1-x)=0,得f(x)=(-x2+4x-3)×1+(x2-1)×0=-x2+4x-3;
②当x=1时,S(x-1)=S(1-x)=1,得f(x)=(-x2+4x-3)×1+(x2-1)×1=4x-4;
③当x<1时,S(x-1)=0且S(1-x)=1,得f(x)=(-x2+4x-3)×0+(x2-1)×1=x2-1
∴f(x)=
(2)函数y=f(x)的大致图象:

(3)若F(x)为奇函数,则F(x)的图象应关于原点对称,
因为k>0时,F(x)=f(x+k)的图象可以看成是把函数f(x)的图象向左平移k个单位得到,
又∵函数f(x)的图象关于点A(1,0)对称,∴只要把函数f(x)的图象向左平移1个单位后,图象就关于原点对称,
∴当k=1时,函数F(x)的图象应关于原点对称,则F(x)为奇函数.
①当x>1时,S(x-1)=1且S(1-x)=0,得f(x)=(-x2+4x-3)×1+(x2-1)×0=-x2+4x-3;
②当x=1时,S(x-1)=S(1-x)=1,得f(x)=(-x2+4x-3)×1+(x2-1)×1=4x-4;
③当x<1时,S(x-1)=0且S(1-x)=1,得f(x)=(-x2+4x-3)×0+(x2-1)×1=x2-1
∴f(x)=
|
(2)函数y=f(x)的大致图象:

(3)若F(x)为奇函数,则F(x)的图象应关于原点对称,
因为k>0时,F(x)=f(x+k)的图象可以看成是把函数f(x)的图象向左平移k个单位得到,
又∵函数f(x)的图象关于点A(1,0)对称,∴只要把函数f(x)的图象向左平移1个单位后,图象就关于原点对称,
∴当k=1时,函数F(x)的图象应关于原点对称,则F(x)为奇函数.
点评:本题以分段函数和二次函数为载体,讨论函数的奇偶性,着重考查了基本初等函数的图象与性质、函数解析式的求解及常用方法和奇偶性与函数平移等有关知识的综合考查.

练习册系列答案
相关题目
对任意x,y满足f(x+y2)=f(x)+2[f(y)]2,且f(1)≠0,则f(2013)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=alog2x+blog4x+2,且f(
)=4,则f(2014)的值为( )
| 1 |
| 2014 |
| A、-4 | B、2 | C、0 | D、-2 |
已知命题p:若2b=a+c,则a、b、c成等差数列;命题q:若b2=ac,则a、b、c成等比数列,则下列命题中是真命题的是( )
| A、¬p或q | B、p且q |
| C、¬p且¬q | D、¬p或¬q |
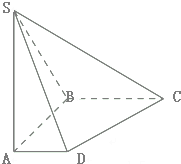 如图,四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
如图,四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=