��Ŀ����
����ԲC��
+
=1��a��b��0�������ҽ���ֱ�ΪF1��F2���϶���ΪA����A��AF2��ֱ��ֱ�߽�x�Ḻ������Q�㣬��2
+
=
��
��������ԲC�������ʣ�
��������A��Q��F2�����Բǡ����ֱ��x-
y-3=0���У�����ԲC�ķ��̣�
����F2��ֱ��l�루������Բ���ڲ�ͬ������M��N�����F1MN������Բ������Ƿ�������ֵ�������ڣ����������ֵ����ʱ��ֱ�߷��̣��������ڣ���˵�����ɣ�
| x2 |
| a2 |
| y2 |
| b2 |
| F1F2 |
| F2Q |
| 0 |
��������ԲC�������ʣ�
��������A��Q��F2�����Բǡ����ֱ��x-
| 3 |
����F2��ֱ��l�루������Բ���ڲ�ͬ������M��N�����F1MN������Բ������Ƿ�������ֵ�������ڣ����������ֵ����ʱ��ֱ�߷��̣��������ڣ���˵�����ɣ�
���㣺ֱ����Բ���ߵ��ۺ�����,��Բ�ı�����
ר�⣺Բ���ߵĶ��塢�����뷽��
��������������A��0��b����F1ΪQF2���е㣮��F1��-c��0����F2��c��0������Q��-3c��0����
=(-3c��-b)ͨ��
��
���г�c�ķ��̣����c�����ɵõ������ʣ�
��������Rt��QAF2���Բ��ֱ�����У��Ƴ�d=r�����c=1��Ȼ�����a��b����������ԲC�ķ��̣�
������M��x1��y1����N��x2��y2�����������F1MN������Բ�İ뾶ΪR���õ���F1MN���ܳ�Ϊ4a=8����ʾ����F1MN����Բ���������ʽ��˵��R���S��F1MNҲ�����ֱ��l�ķ���Ϊx=my+1������Բ������ͨ��Τ�ﶨ��
����S��F1MN=
�����û�������ʽ�����ֵ���ɣ�
| AQ |
| AQ |
| AF2 |
��������Rt��QAF2���Բ��ֱ�����У��Ƴ�d=r�����c=1��Ȼ�����a��b����������ԲC�ķ��̣�
������M��x1��y1����N��x2��y2�����������F1MN������Բ�İ뾶ΪR���õ���F1MN���ܳ�Ϊ4a=8����ʾ����F1MN����Բ���������ʽ��˵��R���S��F1MNҲ�����ֱ��l�ķ���Ϊx=my+1������Բ������ͨ��Τ�ﶨ��
����S��F1MN=
12
| ||
| 3m2+4 |
���
�⣺��������A��0��b����F1ΪQF2���е㣮
��F1��-c��0����F2��c��0������Q��-3c��0��
=(-3c��-b)��
=(c��-b)
����
��
����
•
=-3c2+b2=0����-3c2+��a2-c2��=0��a2=4c2��e=
=
��������Rt��QAF2���ԲԲ��Ϊб��QF2���е�F1��-c��0�����뾶r=2c��������Rt��QAF2���Բ��ֱ��x-
y-3=0����d=r����
=2c����c+3=4c��c=1��a=2c=2��b=
���������ԲC�ķ���Ϊ
+
=1
������M��x1��y1����N��x2��y2��������y1��y2��ţ�
���F1MN������Բ�İ뾶ΪR�����F1MN���ܳ�Ϊ4a=8��S��F1MN=
(|MN|+|F1M|+|F1N|)R=4R��
���Ҫʹ��F1MN����Բ��������ֻ��R���ʱS��F1MNҲ���S��F1MN=
|F1F2|•|y1-y2|=|y1-y2|��
����֪��ֱ��l��б�ʲ�Ϊ�㣬����ֱ��l�ķ���Ϊx=my+1��
��
�ã�3m2+4��y2+6my-9=0��
��Τ�ﶨ����y1+y2=
��y1y2=
��������0⇒m��R��S��F1MN=|y1-y2|=
=
��t=
����t��1S��F1MN=
=
��t��1����
��t=1ʱS��F1MN=4R�����ֵ3����ʱ��m=0��Rmax=
�ʡ�F1MN������Բ����������ֵΪ
����ʱֱ��l�ķ���Ϊx=1
��F1��-c��0����F2��c��0������Q��-3c��0��
| AQ |
| AF2 |
����
| AQ |
| AF2 |
| AQ |
| AF2 |
| c |
| a |
| 1 |
| 2 |
��������Rt��QAF2���ԲԲ��Ϊб��QF2���е�F1��-c��0�����뾶r=2c��������Rt��QAF2���Բ��ֱ��x-
| 3 |
| |-c-3| |
| 2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
������M��x1��y1����N��x2��y2��������y1��y2��ţ�
���F1MN������Բ�İ뾶ΪR�����F1MN���ܳ�Ϊ4a=8��S��F1MN=
| 1 |
| 2 |
���Ҫʹ��F1MN����Բ��������ֻ��R���ʱS��F1MNҲ���S��F1MN=
| 1 |
| 2 |
����֪��ֱ��l��б�ʲ�Ϊ�㣬����ֱ��l�ķ���Ϊx=my+1��
��
|
��Τ�ﶨ����y1+y2=
| -6m |
| 3m2+4 |
| -9 |
| 3m2+4 |
| (y1+y2)2-4y1y2 |
12
| ||
| 3m2+4 |
��t=
| m2+1 |
| 12t |
| 3t2+1 |
| 12 | ||
3t+
|
��t=1ʱS��F1MN=4R�����ֵ3����ʱ��m=0��Rmax=
| 3 |
| 4 |
�ʡ�F1MN������Բ����������ֵΪ
| 9�� |
| 16 |
���������⿼����Բ�Ļ������ʣ�ֱ������Բ��λ�ù�ϵ���ۺ�Ӧ�ã�����ת��˼���Լ�����������

��ϰ��ϵ�д�
 �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
�����Ŀ
��֪����U={x|x��С��18��������}��A�ɣ�∁UB��={3��5}��B�ɣ�∁UA��={7��11}����∁UA���ɣ�∁UB��={2��17}����A= ��
��֪����f��x��=
������g��x��=f��x��-x��������ͬ����㣬��a��ȡֵ��Χ�ǣ�������
|
A��-
| ||
B��a��-
| ||
C��a��-
| ||
D��-
|
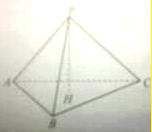 ��ͼ��PΪ��ABC����ƽ����һ�㣬PA��PB��PB��PC��PC��PA��PH��ƽ��ABC��H����֤��H�ǡ�ABC�Ĵ��ģ���ABCΪ��������Σ�
��ͼ��PΪ��ABC����ƽ����һ�㣬PA��PB��PB��PC��PC��PA��PH��ƽ��ABC��H����֤��H�ǡ�ABC�Ĵ��ģ���ABCΪ��������Σ�