题目内容
2．已知点A（$\sqrt{3}$，0）和P（$\sqrt{3}$，t）（t∈R），若曲线x2+y2=3上存在点B使∠APB=60°，则t的最大值为（ ）| A． | $\sqrt{3}$ | B． | 2 | C． | 1+$\sqrt{3}$ | D． | 3 |
分析 由题意，PB与圆相切，∠APB=60°，t取得最大值或最小值，t取得最大值时，tan30°=$\frac{\sqrt{3}}{t}$，即可得出结论．
解答 解：由题意，PB与圆相切，∠APB=60°，t取得最大值或最小值，
t取得最大值时，tan30°=$\frac{\sqrt{3}}{t}$，∴t=3，
故选D．
点评 本题考查直线与圆的位置关系，考查学生的计算能力，属于中档题．
练习册系列答案
习题精选系列答案
相关题目
12．若变量x、y满足$\left\{\begin{array}{l}{x+y≤-1}\\{2x-3y≤9}\\{x≥0}\end{array}\right.$，则x2+y2的最小值是（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | 1 | C． | 3 | D． | $\frac{1}{2}$ |
13．已知点A（-1，2），B（1，-3），点P在线段AB的延长线上，且$\frac{|\overrightarrow{AP}|}{|\overrightarrow{PB}|}$=3，则点P的坐标为（ ）
| A． | （3，-$\frac{11}{2}$） | B． | （$\frac{1}{2}$，-$\frac{11}{4}$） | C． | （2，-$\frac{11}{2}$） | D． | （$\frac{1}{2}$，-$\frac{7}{4}$） |
10．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，O为坐标原点，P是双曲线在第一象限上的点且满足|PF1|=2|PF2|，直线PF2交双曲线C于另一点N，又点M满足$\overrightarrow{MO}$=$\overrightarrow{OP}$且∠MF2N=120°，则双曲线C的离心率为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\sqrt{7}$ | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
14．若x、y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$，且目标函数z=ax+2y仅在点（1，0）处取得最小值，则a的取值范围是（ ）
| A． | （-1，2） | B． | （-4，2） | C． | （-4，0） | D． | （-2，4） |
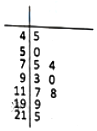空气质量指数（Air Quality Index，简称AQI）是定量描述空气质量状况的指数，空气质量按照AQI大小分为六级，0～50为优；51～100为良；101～150为轻度污染；151～200为中度污染；201～300为重度污染；大于300为严重污染．一环保人士当地某年的AQI记录数据中，随机抽取10个，用茎叶图记录如图．根据该统计数据，估计此地该年AQI大于100的天数约为为146．（该年为365天）